| |
 |
| |
 |
| ● 塑性力学とは |
| 〇 ものづくり 塑性加工 |
| 〇 塑性力学 |
| |
| ● 用語 |
| 〇 応力ひずみ線図 |
| 〇 応力とひずみの関係 1次元 |
| 〇 応力ひずみ線図6種類 |
| |
| ● 降伏条件 |
| 〇 最大主応力が降伏条件 1次元 |
| 〇 トレスカの降伏条件 2次元 |
| 〇 ミーゼスの降伏条件 3次元 |
| 〇 降伏曲面 |
| |
| ● 塑性変形 |
| 〇 全ひずみ理論 |
| 〇 ひずみ増分理論 |
| 〇 レービー・ミーゼスの流れ則 |
 |
| ● 塑性力学とは |
| |
 |
| 〇 ものづくり 塑性加工 |
| |
| 航空機、自動車、バイク、自転車などの乗り物、テレビ、洗濯機、クリーナーなどの家電、PC、携帯、バッグ、フライパン、などなど、いつも使っている「物」は、必ず、原材料を何らかの加工をして製造されたものです。 |
| |
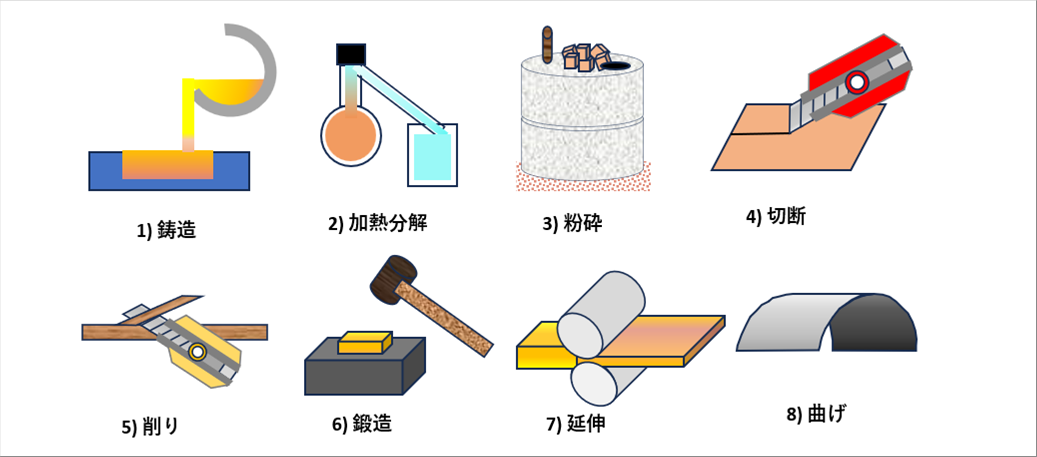
| ものづくりの方法には、1)溶かして型に流し込んで固める鋳造、2)石油などの加熱分解、3) ソバの実を石うすで粉砕、4) カッターでシートを切断、5) 刃物で枝を削る、6) 鉄をたたいて鍛える鍛造、7) 鉄の厚板を伸ばす圧延、8) シートの曲げなど数多くありますが、1), 2)は流体を扱うので、塑性加工ではありません。3)から8)は、固体の形を変え、加工後元に戻りませんので、塑性加工です。下の絵は、それぞれの加工のイメージ図です。 |
| |
 |
| |
| 弾性変形と違い、塑性加工後は、力をなくしても元の形には戻らず、必要な形にとどまります。あらゆるものづくりの基本と言っていいと思います。 |
| |
| |
 |
| 〇 塑性力学 |
| |
| 工場では、最小のエネルギーで最短時間で塑性加工をして、省エネルギー、省資源、低コストを追求しますが、その時に塑性力学が使われます。 |
| |
| 加工時には、摩擦、発熱など、加工に伴う不可避的な「不要物」が発生します。これを最小にすることは有意義です。また、外からの力を除いた時に、元の形には戻りませんが、0.2%程度の弾性変形分は元に戻ろうとします。弾性変形分を考慮してほしい形よりちょっと小さい形にすることも意義があります。 |
| |
| 加工に必要な力、動力がどのくらい必要なのか知ることは非常に重要です。すでに実施している加工量を、ちょっと大きくする場合は、加工量比例などで予測することもできると思いますが、始めてだったり、大きな変革の場合は、「加工量」や「加工の過程」に大きな違いがあるので、経験が活かせない場合もあると思います。 |
| |
| これらを知るための試行錯誤は必須ですが、事前計算である程度予測できれば、試行錯誤の回数を減らせます。この時に使われるのが塑性力学です。 |
| |
 |
| ● 用語 |
 |
| 〇 応力ひずみ線図 |
| |
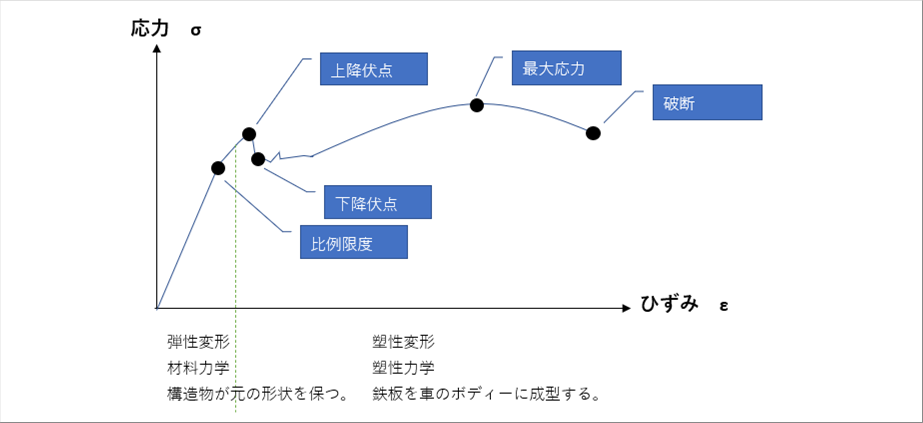
| 応力ひずみ線図は、下の絵の通りです。(材料力学の絵と同じです。) |
| |
 |
| |
| 材料に応力とひずみが発生していて、降伏点より小さい場合は、応力がなくなるとひずみもなくなり、元の形にもどります。降伏点を超えると応力をなくしても、元の形には戻りません。これを塑性変形といいます。 |
| |
| 扱うものによって、応力ひずみ線図は異なりますので、上の絵とは違い、比例限度と上降伏点が同じ場合や、下降伏点がない場合もあります。 |
| |
 |
| 〇 応力とひずみの関係 1次元 |
| |
| 引張試験など、細い棒を1方向に引っ張る場合が1次元の応力ひずみ関係です。前の絵は、1次元の場合と考えていいと思います。応力ひずみ関係は、次の3式で与えられます。 |
| |
| 歪ε = 弾性歪εe + 塑性歪εp |
| |
| 弾性変形中の応力σ = Eεe |
| |
| 塑性変形中の応力σ = F(εp) |
| |
| ここで、E:ヤング率、F:塑性歪を変数とする関数(降伏条件) |
| |
| 歪εが既知で、応力σが知りたい場合、未知数はεe、εp、σの3個で、式が3個なので、F(降伏条件)がわかれば未知数は計算できます。 |
| |
 |
| 〇 応力ひずみ線図6種類 |
| 降伏点以降の応力ひずみ線図が降伏条件Fです。鉄鋼などの解析には、応力ひずみ線図は次のように扱われることが多いと思います。 |
| |
| 1) 剛完全塑性体 |
| |
| 弾性変形なし、降伏点以降、応力一定 |
| |
| 2) 弾完全塑性体 |
| |
| 弾性変形あり、弾性限は降伏点と同じ、降伏点以降応力一定 |
| |
| 3) 線形硬化剛塑性体 |
| |
| 弾性変形なし、降伏点以降、応力は歪に比例して増加 |
| |
| 4) 線形硬化弾塑性体 |
| |
| 弾性変形あり、弾性限は降伏点と同じ、降伏点以降応力は歪に比例して増加 |
| |
| 5) 非線形硬化剛塑性体 |
| |
| 弾性変形なし、降伏点以降、応力は歪に非線形で増加 |
| |
| 6) 非線形硬化弾塑性体 |
| |
| 弾性変形あり、弾性限は降伏点と同じ、降伏点以降応力は歪に非線形に増加 |
| |
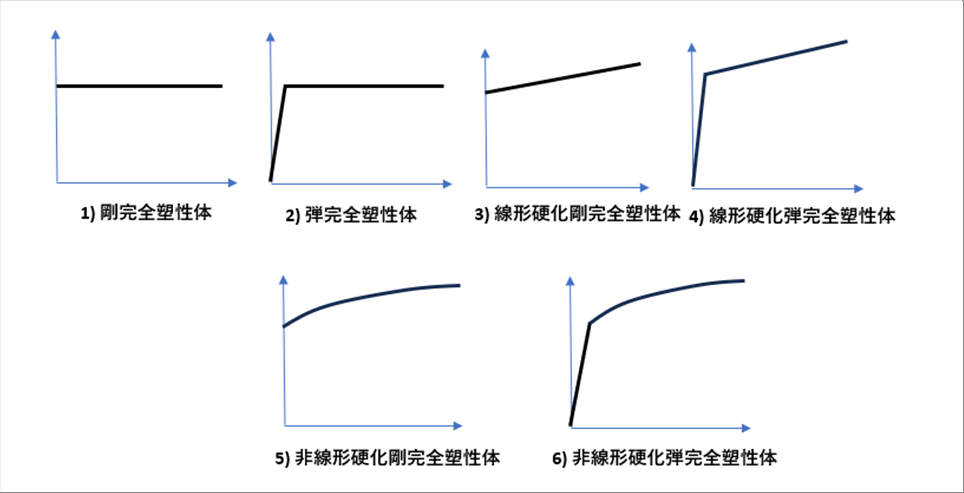
| 応力ひずみ線図の、最大応力までを以上の区分でイラストにすると、次のようになる。どれが正しいというわけではなく、解析に必要なものを選択すればいいと思います。 |
| |
 |
| |
| 炭素鋼材料の加工を考える場合、加熱炉で1200度Cから1300度Cまで加熱してから加工する場合が多く、この温度領域では弾性変形はほとんどありません。さらに、加工中にも再結晶するのでひずみが蓄積されにくく、したがって加工硬化も小さいと思われます。したがって、1)を採用しても差し支えないと思われます。 |
| |
| アルミや、オーステナイト系ステンレスは、5)がいいようです。 |
| |
 |
| ● 降伏条件 |
| |
| どのような応力状態で降伏するかは、3説あります。 |
| |
 |
| 〇 最大主応力が降伏条件 1次元 |
| |
| 最大主応力が、ある値(=降伏応力)になったときに降伏する。 |
| |
| σy = max(σ1,σ2,σ3) |
| |
 |
| 〇 トレスカの降伏条件 2次元 |
| |
| 一般の塑性加工は3次元なので、3次元の降伏条件を考えます。我々の大先輩のトレスカという方が、19世紀の終わりに提唱された有名な降伏条件を、トレスカの降伏条件といいます。トレスカは、円柱の鍛造、押し出しなどの材料変形の観察からこの式を見出したそうです。 |
| |
| トレスカの降伏条件は、最大主応力と最小主応力の差が一定値になると降伏するというものです。式では、次式で与えられます。 |
| |
| σy = σmax ー σmin |
| |
| ここで、最大主応力と最小主応力の差は、最大せん断応力の2倍なので、この式の両辺を2で割って、せん断応力で表現すると次式になります。 |
| |
| 0.5σy = 0.5 (σmax ー σmin) = max(τ1,τ2,τ3) |
| σy = σmax ー σmin = 2 max(τ1,τ2,τ3) |
| |
| ここで、τ1,τ2,τ3は、3次元の最大せん断応力の各成分です。 |
| |
| この式は、最大主せん断応力がある値になると降伏することをしめしています。このため、トレスカの降伏条件式は、最大せん断応力説ともいわれています。 |
| |
| せん断降伏応力をkと書くと、トレスカの降伏条件は次式で表されます。 |
| |
| σy = σmax ー σmin = 2k |
| |
 |
| 〇 ミーゼスの降伏条件 相当応力 3次元 |
| |
| ミーゼスの降伏条件は、3次元を考え、材料の(弾性)せん断歪エネルギーが一定値になると降伏するという説で、下の式で定義されます。なお、エネルギーは、力 X 力の移動距離で与えられ、単位はジュール J です。 |
| |
| σy = sqrt ( 0.5 x ( (σ1 - σ2)^2 + (σ2 - σ3)^2 + (σ3 - σ1)^2 ) ) |
| |
| これは、3次元の物体の主応力から降伏条件が計算できます。Σy は、相当応力、ミーゼス応力などと呼ばれています。 |
| |
| 引張試験のような1次元の場合、σ2 = σ3 = 0なので、σy = σとなり、最大主応力で降伏するという1次元の降伏条件と同じになります。 |
| |
| 一般のxyz3次元で表現すると次式になります。 |
| σy = sqrt( (σx - σy)^2 + (σy - σz)^2 + (σz - σx)^2 + 6(τxy^2 + τyz^2 + τzx^2) ) |
| |
 |
| 〇 降伏曲面 |
| |
| 最大主応力、トレスカの降伏条件、ミーゼスの降伏条件の3つをグラフ表示したものが降伏曲面と呼ばれるものです。降伏曲面を見ながら、度の応力がどのように変化したら降伏するかが考察できます。 |
| |
| 3次元では複雑なので、2次元で考えます。2次元の応力状態は、平面応力状態と言います。それぞれの定義式から、降伏条件のグラフの形状は次のようになります。 |
| |
| 最大主応力説では、四角形になります。 |
| |
| トレスカの降伏条件は、45度傾いたダイアモンド状になります。 |
| |
| ミーゼスの降伏条件は、45度傾いた楕円形になります。 |
| |
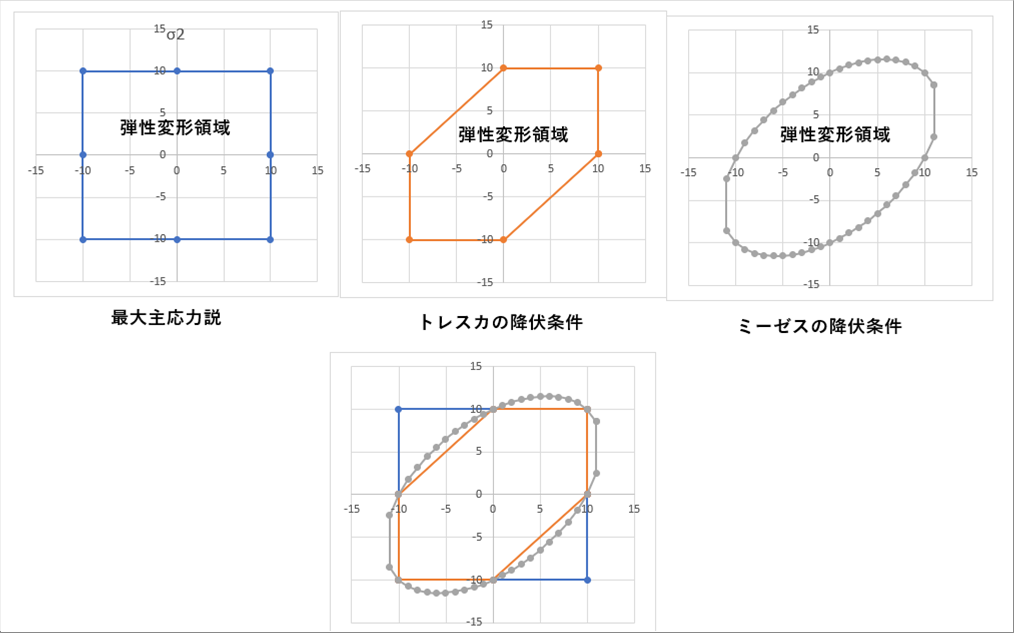
| 降伏条件σy = 10 として、便宜的にエクセルでグラフを作りました。グラフの内部の応力状態は弾性変形で、線上で降伏し、塑性変形します。 |
| |
 |
| |
| 3説を同じグラフに重ねると最後のグラフになります。 |
| |
| トレスカの降伏条件が、3説の中で一番内側にあるので、最も厳しめに判定ができます。 |
| |
| ミーゼスの降伏条件は、第1,第3象限(グラフの右上と左下)では最大主応力説より若干大きくなっていますが、第2、第4象限(右上と左下)では、小さくなっています。 |
| |
| どの説を採用するかは、設計者の判断によりますが、シミュレーションと相性がいいミーゼスの降伏条件を採用している傾向にあるようです。 |
| |
 |
| ● 塑性変形 |
| |
| 塑性変形を考えることは、固体が変形していく様を、どう表現するかということになります。我々の大先輩が提案されたものは、最終形のみに注目する理論と、変形の各過程でのひずみ増分とその時の相当応力に着目した理論があります。 |
| |
| 後者は、流体力学の考え方から来ています。最初に「流体は、力が無くても自由に変形するので塑性加工では除外する。」と、言っておきながら矛盾しているように思えますが、外力により固体が降伏し、変形中の様子は、流体力学の考え方が適用できるのではないかと提案されたそうです。 |
| |
 |
| 〇 全ひずみ理論 |
| |
| 塑性変形は、塑性歪と偏差応力の最終地だけによって決まるという理論。 |
| |
 |
| 〇 ひずみ増分理論 |
| |
| 塑性変形の各段階で、塑性ひずみ増分が、その時の偏差応力の関数となっているとする理論。 |
| |
 |
| 〇 レービー・ミーゼスの流れ則 |
| |
| 塑性力学で有名なレービー・ミーゼスの切に「流れ」が入っていますが、流体力学を応用しているからです。 |
| |
| 応力とひずみの関係は、前出の次式で表されます。 |
| |
| 歪ε = 弾性歪εe + 塑性歪εp |
| |
| この式を3次元に適用します。歪を増分で表すと、次式になります。 |
| |
| 歪増分 dε = 弾性歪増分 dεe + 塑性歪増分 dεp |
| |
| 塑性変形中の固体の流れを流体のように扱う具体例は、非圧縮性流体の体積一定の条件と、粘性力の式です。(詳細は、流体力学参照。) |
| |
| dεp = dεxp x + dεp y +dεp z = 0 |
| |
| これは、非圧縮流体の体積一定の条件と同じです。 |
| |
| 流体の粘度をμ、せん断力をτ、速度勾配をv’とすると、せん断力τは次式で表されます。 |
| |
| τ = μv’ |
| |
| レービー・ミーゼスの流れ則は、これと似ています。相当応力と歪増分の関係を次式で表現します。 |
| |
| σ' = 2με' |
| |
| dε1 / σ'1 = dε2 / σ'2 = dε3 / σ'3 |
| |
| 流体の粘度 μ = τ/ v' は、一定ですが、レービー・ミーゼスの流れ則では、この比は、常に一定値ではありません。 |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| Author: T. Oda |
| このページは、excel2webで自動作成しました。 |











































