| |
 |
| |
 |
| ● 速度と圧力の分布 |
| 〇 速度分布 |
| 〇 圧力係数分布 |
| ● 計算方法 |
| 〇 円柱周りの速度分布の式 |
| 〇 円柱周りの圧力分布の式 |
| ● 実際の流体との違い |
| 〇 円柱周りの粘性流体 |
| |
 |
| ● 速度と圧力の分布 |
| |
 |
| 〇 速度分布 |
| |
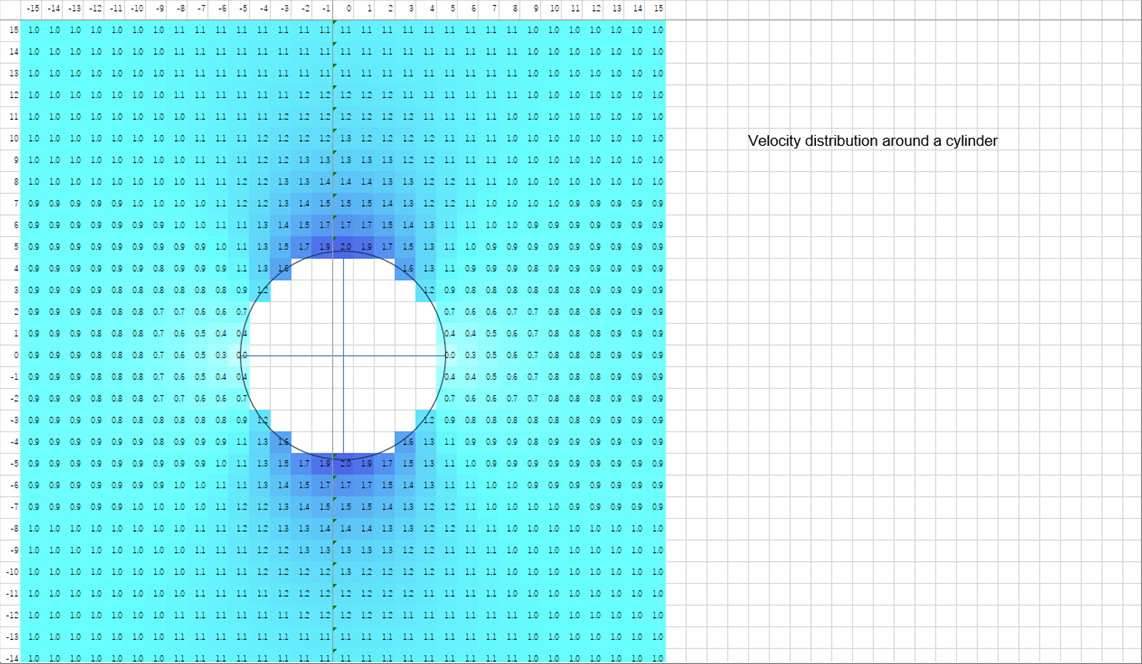
| 下の絵は、後述する特殊な条件下での円柱周りの速度分布を計算した結果を、エクセルでヒートマップチャート状に表示したものです。左から右に流れる流体の中に円柱が静止しています。円柱から十分離れた距離の流体速度は一様に速度1です。計算結果の色が薄いと遅く、色が濃いと速い流れを意味しています。チャートを見ればわかりますが、速度分布は、円柱の水平軸と垂直軸に対して、上下と左右で対象になります。円柱の左右直径の表面速度が最小(0)で、上下直径の位置の表面速度が最大(2)になります。 |
| |
 |
| |
 |
| 〇 圧力係数分布 |
| |
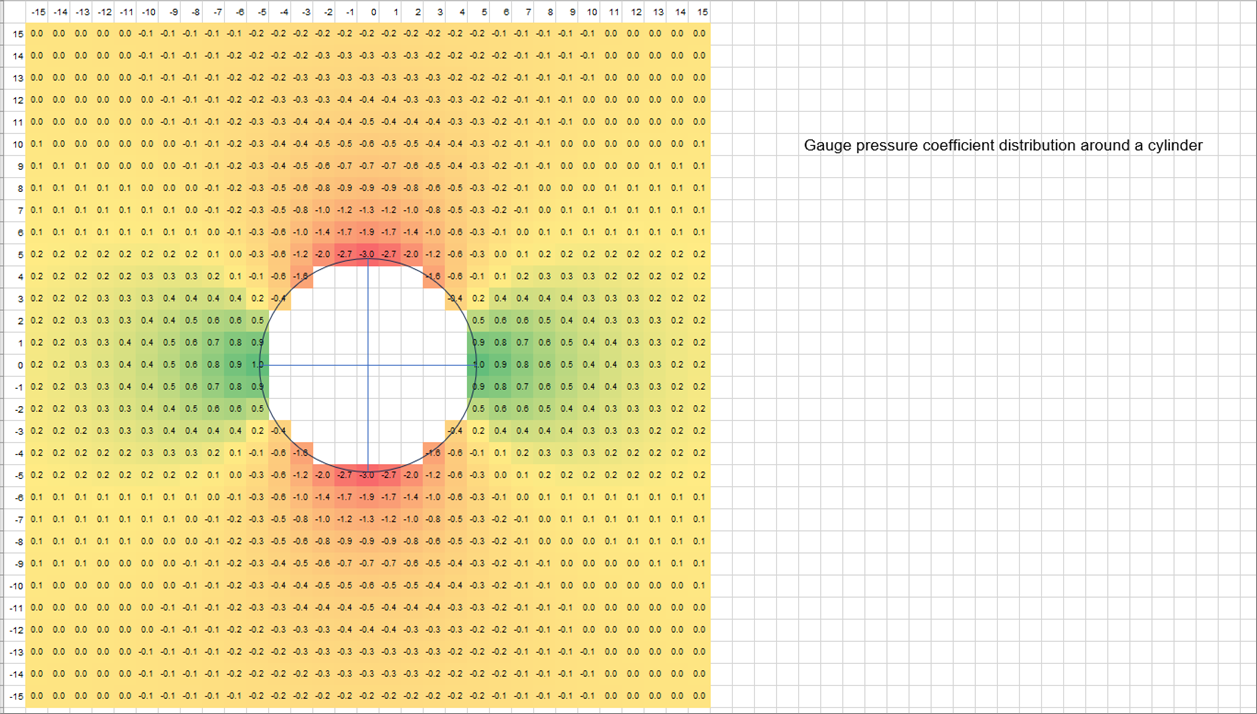
| 同じ場所の静圧と動圧の比率を圧力係数といいます。ここでは、静圧をゲージ圧とします。(ゲージ圧=絶対圧力と環境の圧力の差)下のチャートは、圧力係数のヒートマップです。マイナスが赤、プラスが緑、中間を黄色にしています。緑の部分は環境より圧力が高く、赤の部分は環境より圧力が低いと見ていいと思います。速度分布と同様に、圧力係数も上下左右で対象で、円柱から十分離れた位置でゼロ、円柱表面の最小値は上下部分でー3,最大値は左右部分で1です。 |
| |
 |
| |
| |
 |
| ● 計算方法 |
| |
| 流体の運動方程式であるナビエ・ストークス方程式は次式で与えられます。詳細は、「ナビエ・ストークス方程式の導出」を参照してください。 |
| |
 |
| |
| |
| また、特定の条件下でのエネルギー保存則がベルヌイの定理で、次式で与えられます。特定の条件とは、同一流線上の2点で、エネルギー量に変化がない場合をさします。詳細は、「ベルヌイの定理」を参照ください。 |
| |
 |
| |
| 流れには状態と性質によって下の表のように区分できます。 |
| |
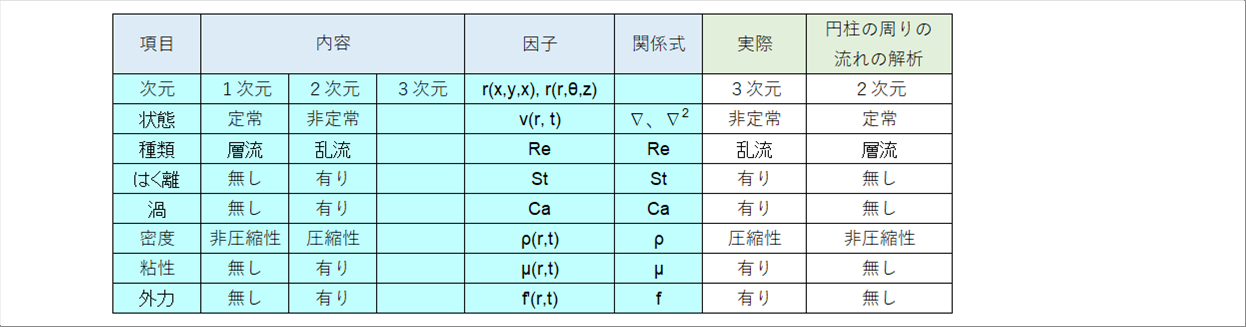 |
| 円柱周りの流れを考えるため、2次元、非圧縮性、定常、非粘性流を考えます。条件が多すぎると思われるかもしれませんが、大胆な仮定がないと解析的に解けないのでご了承ください。これが、最初にお断りした「特殊な条件下」です。 |
| |
 |
| 〇 円柱周りの速度分布の式 |
| |
| ベルヌイの定理より、円柱の周りの速度は、次式で与えられます。 |
| |
 |
| |
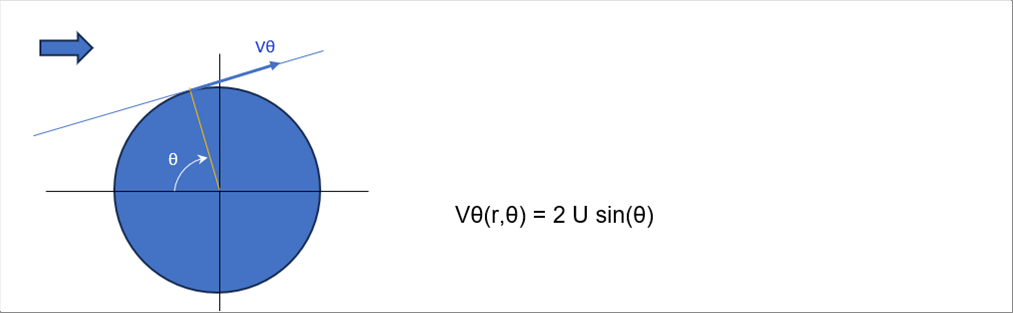
| 円柱表面では、a=r なのでVr=0。接戦方向の速度は、次式となります。 |
| |
 |
| |
| |
| |
| |
 |
| 〇 円柱周りの圧力分布の式 |
| |
| 円柱は、高さ方向(Z)が同一で、圧力損失がないと仮定すると、ベルヌイの式は次式で与えられます。「流体の静圧と動圧の和は一定」と表現したり、「流体の圧力と運動エネルギーの和は一定」と言ったりします。 |
| |
 |
| |
| 静圧の増分と動圧の比(圧力差と運動エネルギーの比)を圧力係数といい、次式で表されます。 |
| |
 |
| |
 |
| ● 実際の流体との違い |
| |
| 川の橋の橋脚には川から力が働きます。この計算では、円柱に働く圧力が上下、左右で対象で釣り合っているので、円柱には力が動きません。こんなことはありえません。 |
| |
| ポールの旗は、風でなびきます。これは、ポールの後面で渦が発生して、この渦が旗を動かしています。計算では、渦は発生しません。 |
| |
| 簡便に計算するために特殊な条件を置きましたが、粘性の影響が大きいと考えられます。粘性以外の項目は作り出せますが、粘性がない流体はありません。 |
| |
 |
| 〇 円柱周りの粘性流体 |
| |
| 未知数は速度と圧力で、円柱の周りの場合は未知数3(平面なので速度2成分、圧力1)です。適用する方程式は、非圧縮性流体のナビエ・ストークス方程式と連続の式です。ナビエ・ストークス方程式は成分ごとにあるので、方程式も3個になります。 |
| |
 |
| |
| 未知数と方程式の数が同じなので解けるはずですが、ナビエ・ストークス方程式の成分の式は複雑で、かつ、2階微分なので解析的には解けません。 |
| |
| 円柱の内部(パイプ)の流れであれば、さらなる簡略化が可能なので、解析的に解くことができます。計算方法と計算結果は「並行平板、円管内の流れ」を参照してください。 |
| |
| |
| Author: T. Oda |
| このページはエクセルで作り、excel2webでhtmlとcssを自動作成しました。 |







































