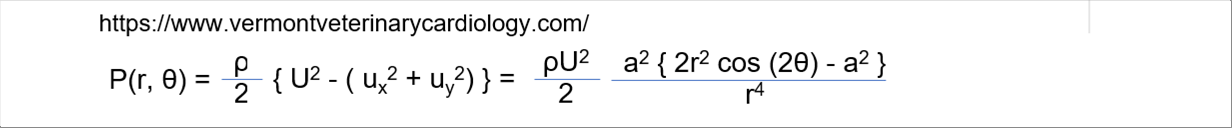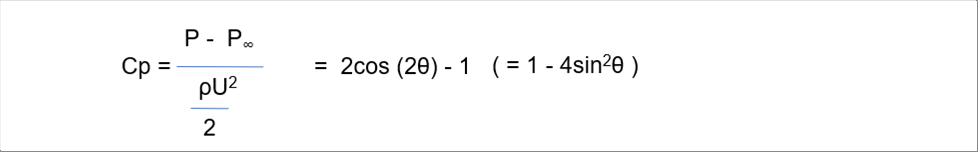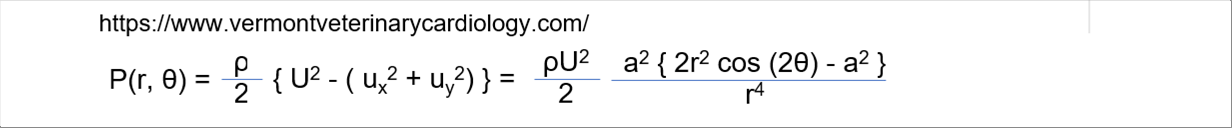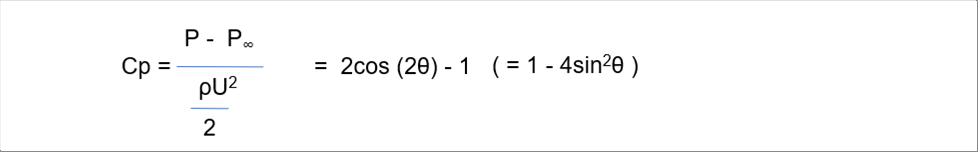| |
 |
| |
 |
| 1 Japan Ministry of Agriculture, Forestry and Fisheries Website |
| 2 Vortex Shedding |
| 2-(1) Vortex Flow Meter |
| 2-(2) Vortex Generator |
| 3 Flow Around an Object |
| 3-(1) Velocity Distribution |
| 3-(2) Pressure Distribution |
| 4 Cavitation and Water Hammer |
| 4-(1) Cavitation |
| 4-(2) Cavitation Number Ca |
| 4-(3) Cavitation of Water |
| 4-(4) Water Hammer |
| 4-(5) Cavitation due to Water Hammer |
| |
 |
| 1 Japan Ministry of Agriculture, Forestry and Fisheries Website |
| |
| The website describes the calculation procedures for cavitation and water hammer countermeasures. The author thinks it will be helpful in practice. |
| |
| The address may be redirected to a fraudulent site when clicked, so the author will paste it graphically. (The internal links in TS Consulting's menu supports tabnabbing as a measure against phishing scams.) |
| |
 |
| |
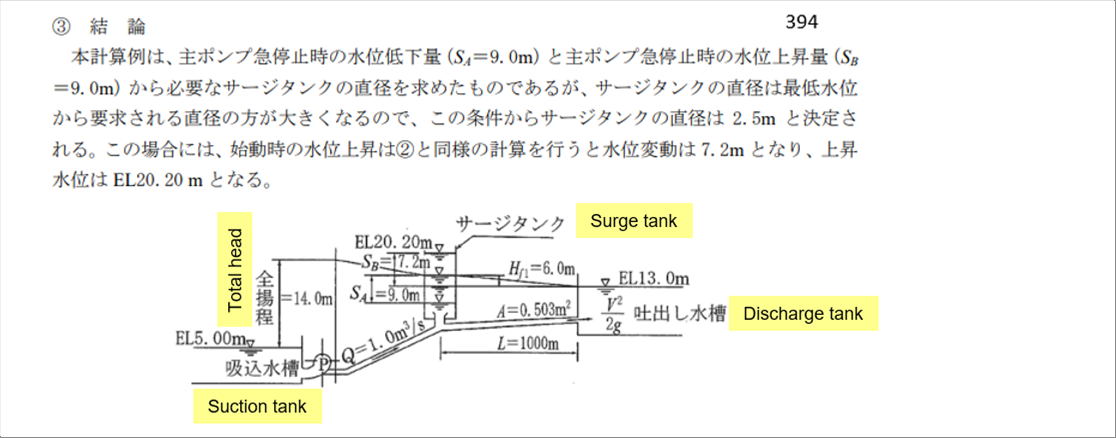
| According to the website, under the given conditions, the conclusion is as follows. (The diameter of the surge tank required was determined from the amount of water level drop at the sudden stop of the main pump and the amount of water level rise when the main pump suddenly stopped. Since the diameter of the surge tan is larger than that from the lowest number, the diameter of the surge tank is determined to be 2.5 m from this condition. In this case, the water level rise at the start is 7.2m in water level fluctuation, and the rising water level is EM20.20m.) |
| |
 |
| |
| On this homepage, the author would like to explain in an easy-to-understand way what fluid vortecies, cavitation, and water hammer are, rather than explaining the calculation procedures. |
| |
 |
| 2 Vortex Shedding |
| |
| Vorticies occur when fluid flowing along an object separetes from an object due to a faster flow velocity. For example, flags flutter in wind, a power line growls in wind, or water plants around a bridge pier sway. |
| |
| As shown in the picture below, when a wind hits an object of circular cross-sectional section, alternately and regularly forming vortices on the rear surface. The is called the von Karman vortex street. Vortices are generated in a regular manner, so the air vibrates and can be heard as a sound of wind. When it hits a thing tree branch, we hear the high sound, and on thick tree trunks we hear a low sound. As we experienced, the pitch also changes depending on the wind velocity. |
| |
 |
| |
 |
| 2-(1) Vortex Flow Meter |
| |
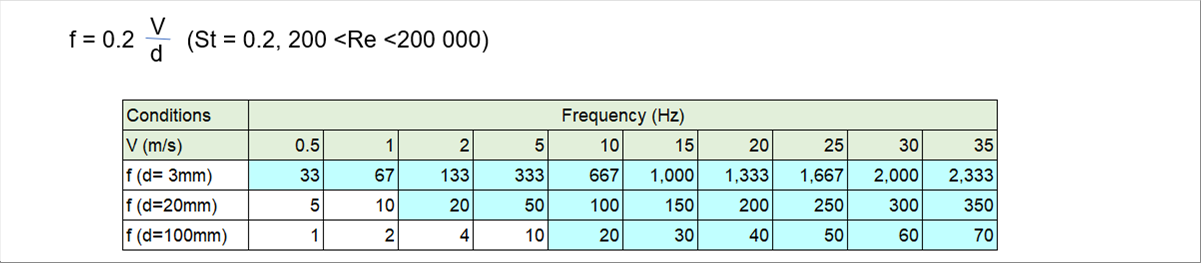
| An example of actively use of vortecies. The vortex flow meter focfibly generates vortecies and measures the flow velocity from the generation cycle. The frequency of the sound due to the von Karman vortex street is given by; |
| |
 |
| |
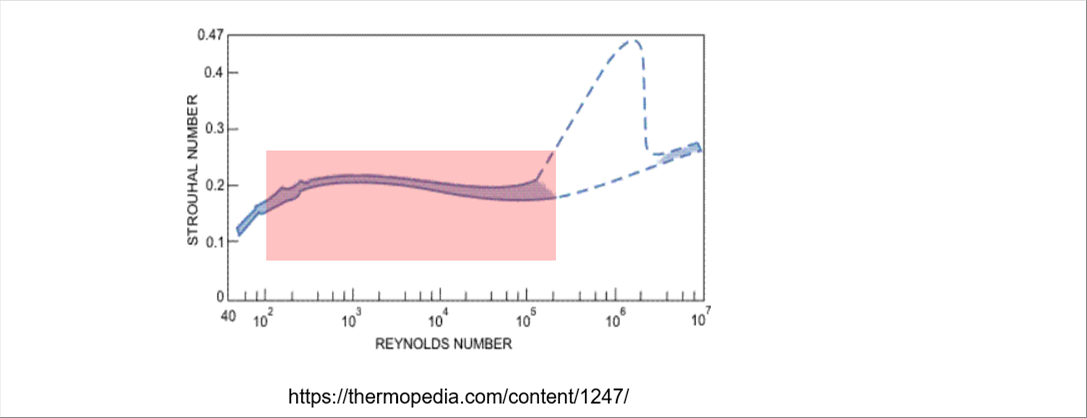
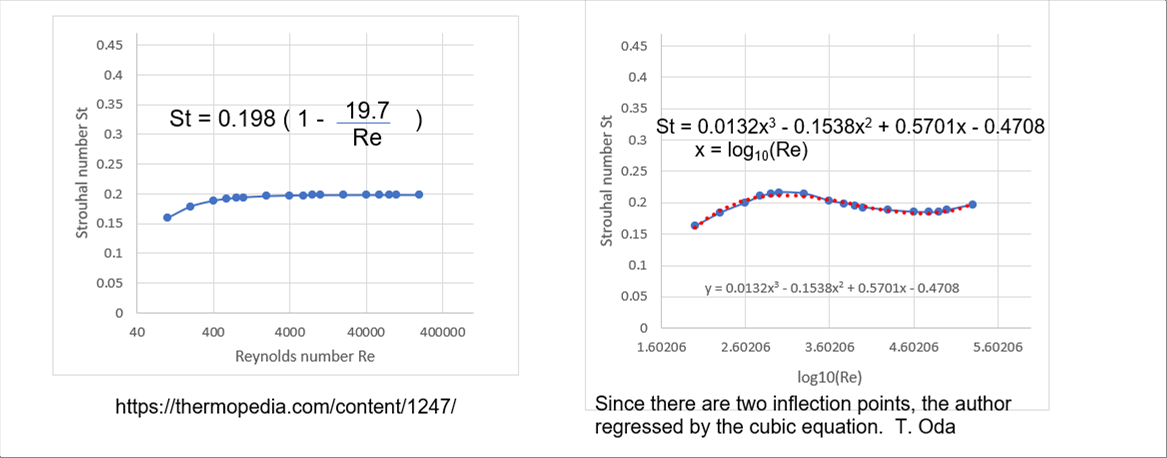
| Here, St is called the Strouhal number, which is related to the Reynolds number. In an experiment, the relationship was shown in the diagram below. |
| |
 |
| |
| The Strouhal number in the red area can be approximated by the function of the reciprocal of the Reynolds number. The author read the numbers from the diagram and made a regression equation. On the left is the website equation, and on the right is the third-order regression equation. |
| |
 |
| |
| The vortex flow meter measures the relationship between the frequency and flow velocity of the vortex generator used in the meter and makes a similar formula, and at the time of measurement, the author thinks that the velocity is calculated from the Strouhal number and the frequency of the sound. |
| |
 |
| 2-(2) Vortex Generator |
| |
| In the 1930s, it was empirically known that fold balls with dimples had a long range. Since the turbulent boundary layer is harder to shed off than the laminar flow boundary layer. So, vortex generators are used to reduce air shedding from aircraft wings, increase lift, and improve the effectiveness of rudders and stabilizers. |
| |
| Some cars have small streamlined protrusions on the door mirrors, rear blinkers on the outside body, and roof ends. They are called vortex generators that generates small vortices to prevent cars from vibrating and behaving unstable due to large swirls that occur unexpectedly. It also has the effect of reducing air drag when driving high speed. |
| |
 |
| |
 |
| 3 Flow Around an Object |
| |
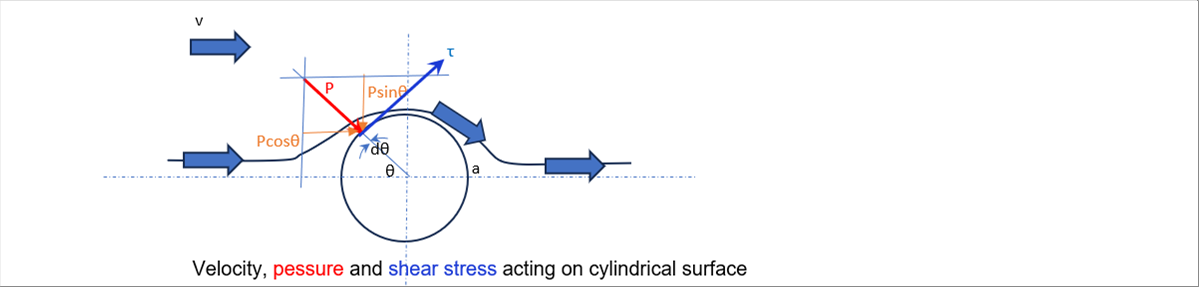
| Assuming zero viscosity and impressibility, the flow around an object is as shown in the picture below. In this condition, the shear force is zero. Solving Bernoulli's equation, we get the formula for pressure. Integral pressure can calculate the fluid force exerted on the body. However, it will be zero. (So, the author will omit the details.) |
| |
 |
| |
| When the Reynolds number is twenty (20) or less, it seems to flow as in the picture above. But when the sound of the wind is heard or flags are flattering, the Reynolds number is larger, and the flow separates form the object surface on the back surface of the object, and the von Karman vortex street occurs. |
| |
 |
| 3-(1) Velocity Distribution |
| |
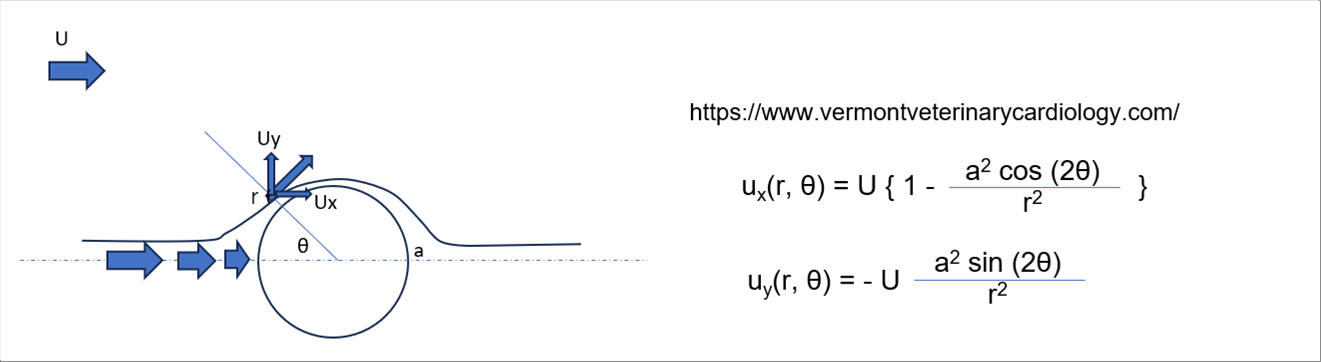
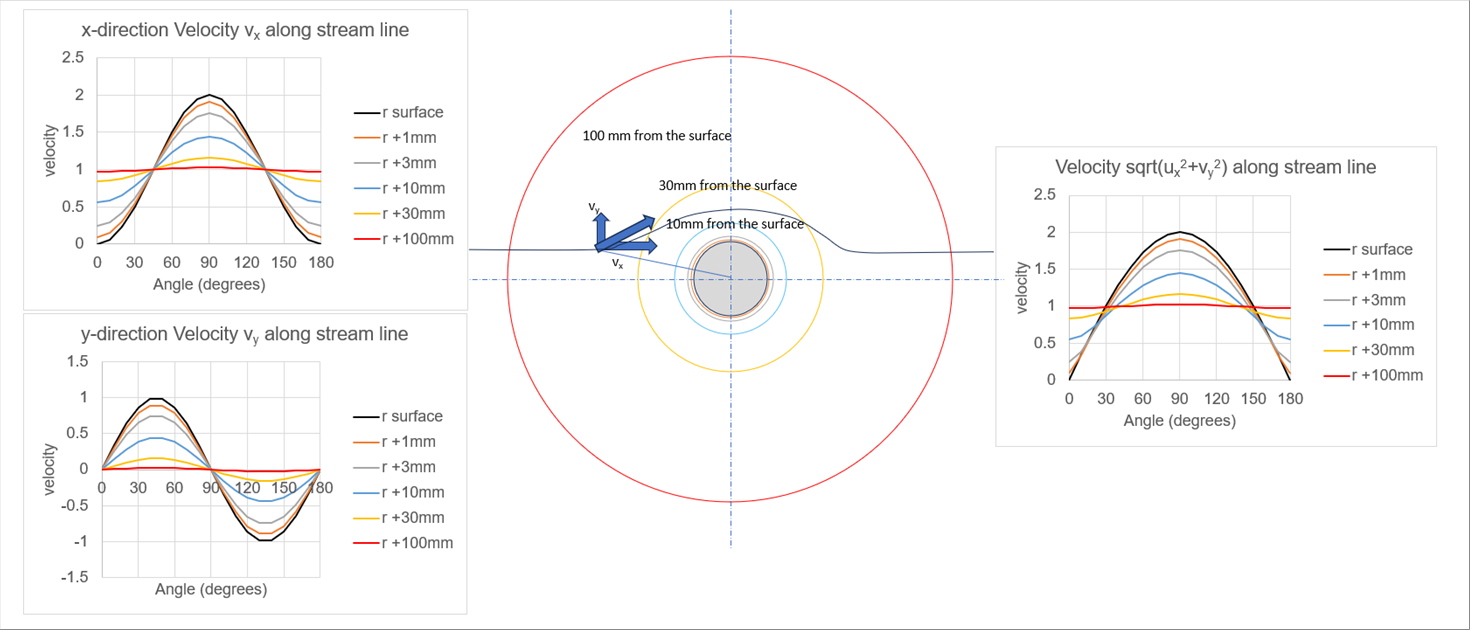
| The velocity distribution around a cylinder is given by: |
| |
 |
| |
| The dimensionless graph with velocity U at a sufficiently distant distance is as follows. The velocity distribution for a radius of a-20mm is calculated as below at the distance from the cylinder surface. The angle is zero (0) is the leftmost point of each graph. The x-directional dimensionless velocity is almost one (1) at a distance of 100 mm. |
| |
 |
| |
 |
| 3-(2) Pressure Distribution |
| |
| From Bernoulli's equation, the pressure distribution is given by: |
| |
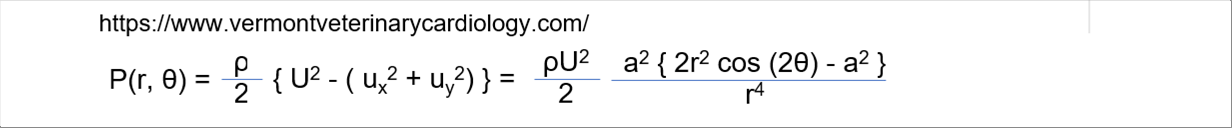 |
| |
| U is the velocity far enough away from the cylinder surface. Taking into account the pressure at that point, the pressure distribution on the object surface r=a is as follows. |
| |
 |
| |
| In order to see the pressure change with angle, let's consider the index in the following equation. |
| |
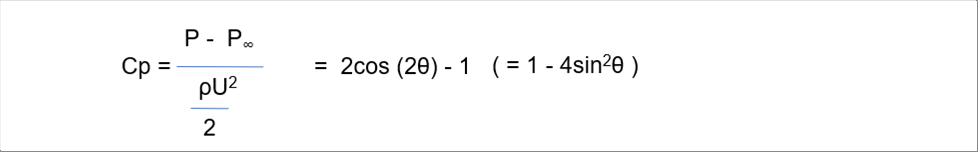 |
| |
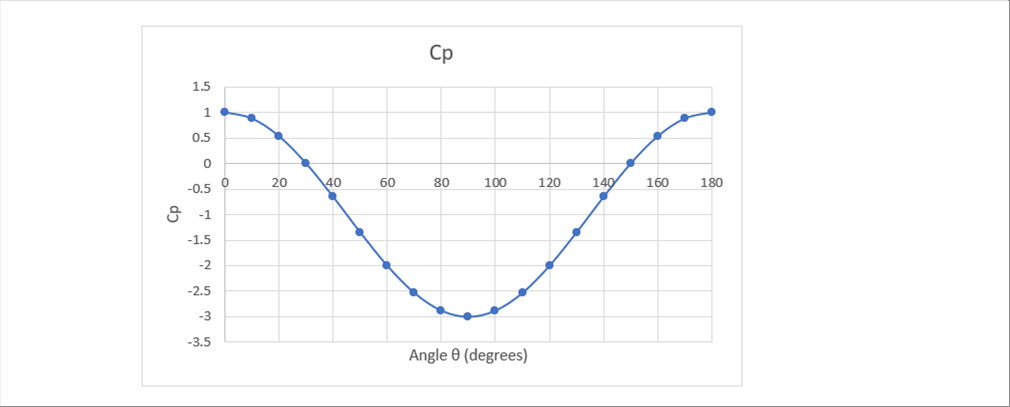
| The following graph shows the Cp with angle. |
| |
 |
| |
| Cp is zero at an angle of thirty (30) degrees, and up to one hundred and fifty (150) degrees it is negative. It has been suggested that when the pressure is negative, the flow will detach from the object somewhere. |
| |
| Now, let's recall the Strouhal number St. It is given as a function of Reynolds number Re. St is roughly 0.2 in the range of 200
|
| |
 |
| |
| it seems that the smaller the diameter, the higher the sound, and the faster the wind velocity, the higher the sound. The fact that there is sound means that the von Karman vortex street has been formed. So, the flow is separated form the object. The author is sorry for those who expected a procedure to find the condition by mathematical formula, but fluid analysis is so complicated and the author used it as a qualitative explanation. |
| |
 |
| 4 Cavitation and Water Hammer |
| |
 |
| 4-(1) Cavitation |
| |
| Bubbles (cavities) that occur in a short time due to pressure difference in the flow of a liquid are called cavitation. Air bubbles form and disappear in a short time. |
| |
 |
| |
| When cavitation occurs, problems such as reduced pump (propeller, screw type) capacity and breakage by shock waves during extinction occur. |
| |
| Depending on where the pump is used, insufficient roll cooling, insufficient thrust, etc. will appear. Conversely, in many cases, it is not known until it becomes apparent, and even it does, it may be assumed that other factors are the main cause. (Personal reflecting is also included.) |
| |
| There are some causes of cavitation, such as high flow velocity and improper flow path. But since the conditions for cavitation are known, it is possible to take actions in advance. |
| |
| In the unlikely event that something in the liquid is damaged, it is important to check whether the conditions for cavitation were there. So, the author thinks it is a good idea to describe it in a maintenance manual. |
| |
 |
| 4-(2) Cavitation Number Ca |
| |
| The inside of the cavitation bubble is saturated with liquid vapor. The dimensionless number of the difference between liquid pressure and vapor pressure is called the cavitation number, and cavitation occurs when Ca = 1. |
| |
| The cavitation number Ca can be obtained by Bernoulli's equation. |
| |
 |
| p = pv + 0.5 ��u^2 |
| Ca = ( p - pv ) / ( 0.5 ��u^2 ) |
| p: Absolute pressure, pv: Vapor pressure, 0.5��u^2: dynamic pressure (representative pressure) |
| ��: Density of fluid, u: Flow velocity |
| |
 |
| 4-(3) Cavitation of Water |
| |
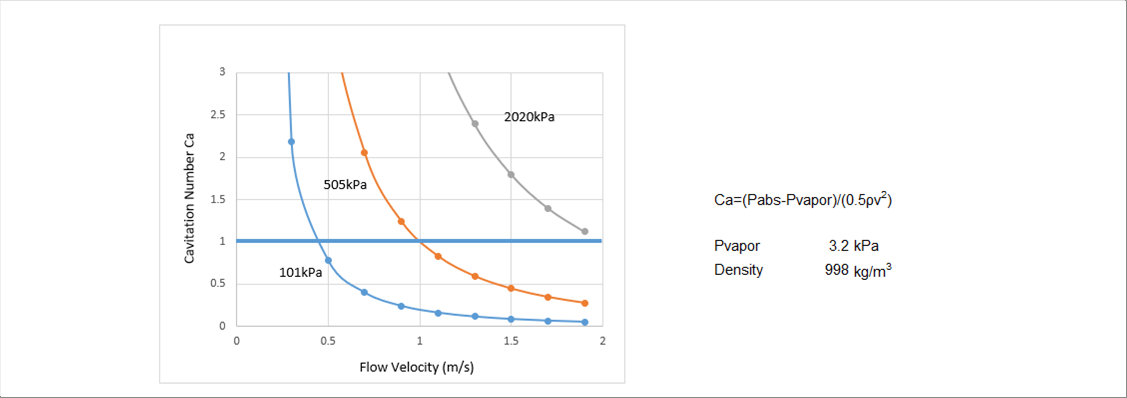
| The graph below shows the result of calculating the cavitation number of water with different pressures. |
| |
 |
| |
| At 10 kPa (atmospheric pressure level), Ca =1 at a low velocity of abut 0.5 m/s. At 505 kPa(the approximate pressure level of tap water), Ca = 1 at 1 m/s. Ca = 1 does not always cause problems, but it can be cause. |
| |
| In order to get Ca<1 at the required velocity, increase the pressure. When the pressure is large, the diagram moves to the upper right like the gray line, so with 2020 kPa, the velocity where Ca=1 becomes 2 m/s. |
| |
| Ways to increase the pressure is to install the pipe at the lowest possible position and to make a circuit that can replenish water from a separate tank or accumulator. If pressure cannot be applied, it may be effective to reduce the flow velocity by increasing the pipe diameter. |
| |
 |
| 4-(4) Water Hammer |
| |
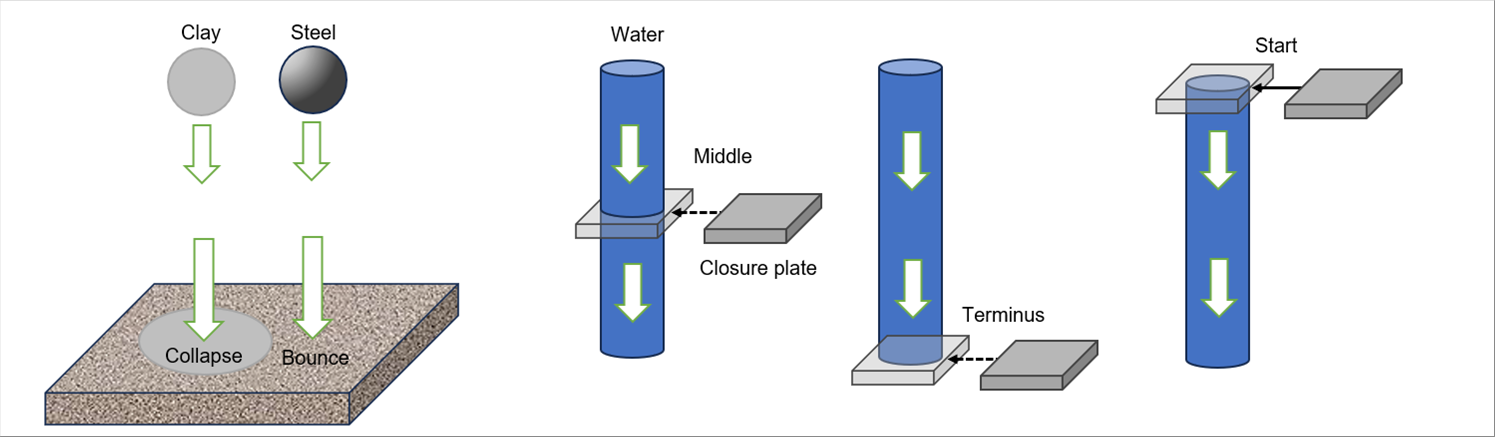
| When an apple falls from a tree and crashes into the ground, its velocity suddenly drops to zero (0), causing an impact. The flid version of the same phenomenon is water hammer. First of all, let's consider the impact of solids. The degree of impact of a solid depends on the degree of "suddenly". It can be measured in time. If we define the impact load by how many seconds the momentum just before crashing becomes zero (0), for example, clay takes 0.5 seconds to collapse itself, while a steel ball bounces back after 0.01 seconds. Momentum is the product of mass and velocity. If the mass and velocity of the clay and the ball are the same, it is inversely proportional to the velocity ratio. The impact load of the iron ball is fifty (50) times the clay. |
| |
| Fluid water hammer is an impact that occurs due to the inertia of a fluid when the flow in a pipe is abruptly stopped. Unlike solids, the continuum is invisible to our eyes, so sound examples are often used. When we suddenly close the lever-type water faucet in our home from full open, we will hear a clicking sound and, in some cases, at the same time, even in the wall. The sound in the wall may be due to the piping is shaking and hitting something if the piping is not fixed well, but these are caused by water hammer. |
| |
 |
| |
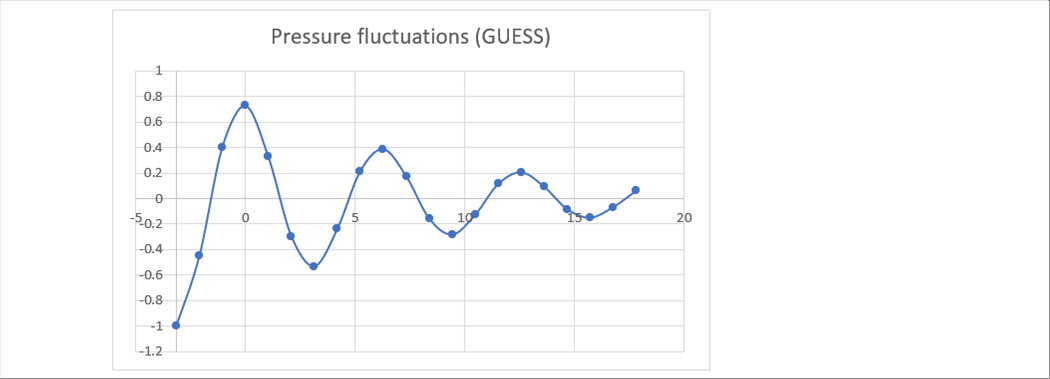
| Clay absorbs impact force and collapses, while steel ball absorbs part of the impact force and bounce with the rest. Gradually the bounce becomes smaller, and eventually it falls down and stops, similar to clay. The same phenomenon occurs when we stop the fluid. Compressible fluids will have a higher density in the area that hits the closing plate, and the density apart from the plate will decrease accordingly. In addition, it is assumed that the pressure fluctuates, and the fluid itself may vibrate. Incompressible fluid do not change density, but it is assumed that the pressure fluctuates. In both fluids, the change decays and eventually stops. The first pressure increase is the largest, which is called water hammer. |
| |
 |
| |
 |
| 4-(5) Cavitation due to Water Hammer |
| |
| Pressure fluctuation occurs due to the water hammer. If the negative pressure is the cavitation generation pressure, cavitation occurs. |
| |
| when cavitation occurs, part of the fluid becomes a gas and the fluid is cut off, which is called the water column separation. Since cavitation and water hammer are problems on their own. The water column separation, where the two (2) phenomena occur at the same time, is likely to develop into a major problem. |
| |
| In addition to the cavitation prevention measures described above, measures to prevent sudden stop of the flow are required. For example, flywheels are used to prevent the pump from stopping abruptly in the event of a power loss. |
| |
| On the website of the Ministry of Agriculture, Forestry and Fisheries, which the author introduced at the biggening, describes in detail the calculation procedures for water hammer countermeasures such as surge tank and flywheel, so please refer to it. According to the website, air chamber is also effective. |
| |
| |
| |
| Author: T. Oda |
| The page was prepared in Excel, and html and css files were automatically generated by the excel2web. |