| |
 |
| |
 |
| ● 工場で使う空気 |
| ● 空気の物性値 |
| ● 粘度、動粘度の温度依存性 |
| ● 比熱、熱伝達率、熱拡散係数の温度依存性 |
| ● 回帰式 |
| ● プラントル数の温度依存性 |
| ● 密度、熱拡散係数、粘度の回帰式の評価 |
| ● 比熱の回帰式の評価 |
| |
 |
| ● 工場で使う空気 |
| |
| 空気は普通の生活していると、文字通り「空気のように」存在していて、その存在を意識することはほとんどありませんが、工業的には、加圧して呼吸器やエアブローに使ったり、空圧機器を動かしたりします。また、バーナーで燃料を燃やして燃焼空気を作り鋼片やパイプを加熱したりと、いたるところで利用されています。 |
| |
| 工業的に空気を使用する際、具体的には、空気を流して何かの仕事をさせる場合、空気を熱を伝達する媒体として扱う場合ともに、使用温度での性質が重要になります。 |
| |
| 空気は窒素、酸素、ほかの混合物質で、通常の温度範囲では気体ですが、冷却すれば液体、固体となります。空気は、シームレスパイプ製造工場では気体状態で利用することが多いですが、温度によって性質が変わるのでどの数値を使うか注意が必要となります。 |
| |
| 性質として、ここでは密度、比熱、粘性率(粘度)、動粘性率(動粘度)、熱伝導率、熱拡散率、プラントル数の温度依存性を理解したいと思います。これらは、流体力学、熱力学で重要な項目でもあります。 |
| |
| 水の物性も温度依存性があるので、熱交換器などでは留意する必要があると思いますが、操業オペレーション的には水の物性を気にする必要がある場合は少ないのでここでは割愛します。 |
| |
 |
| ● 空気の物性値 |
| |
| 空気の物性値の主なものは、密度ρ、低圧比熱Cp、粘度μ、動粘度ν、熱伝達率λ、熱拡散率α、プラントル数Prなどです。流体力学、熱力学で扱う物性値ですが、独立なのは4つだけで(密度ρ、低圧比熱Cp、粘度μ、熱伝達率λ)、残りはそれらから計算された数値です。 |
| |
| 動粘度ν、熱拡散係数α、プラントル数Prは下式で定義されます。 |
| ν=η/ρ |
| α=λ/(ρCp) |
| Pr=ν/α |
| それぞれの意味するところなどは、流体力学、熱力学を参照してください。 |
| |
 |
| ● 粘度、動粘度の温度依存性 |
| |
| 粘度、動粘度の温度による数値は公開されているものがありますので、そちらを参照してください。若干の差はあると思いますが、どの数値を用いるべきかはここでは対象外とします。次のグラフは、絶対値の是非ではなく、シミュレーションや計算で便利なように定式化するためのものです。 |
| |
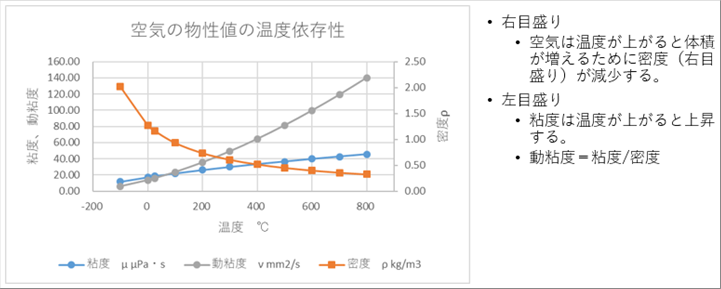 |
| |
| 空気は、温度が上がると体積が増えるために密度ρが小さくなり、粘度μは大きくなります。動粘度νは粘度ρを密度μで割ったものですが、密度が小さくなる影響を大きく受けて、大きくなります。 |
| |
 |
| ● 比熱、熱伝達率、熱拡散係数の温度依存性 |
| |
| 下のグラフは、比熱、熱伝達率、熱拡散係数の温度依存性を示しています。 |
| |
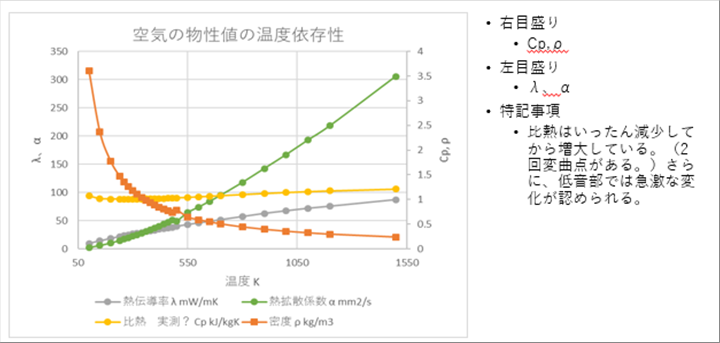 |
| |
| 比熱Cpはほとんど変化していませんが、いったん小さくなり、その後大きくなっています。熱伝導率は温度が上がるにつれて大きくなっています。熱拡散係数は熱伝導率を密度と比熱で除算した数値ですが、温度の上昇により増大しています。 |
| |
 |
| ● 回帰式 |
| |
| 回帰式があると計測点以外の数値も計算できるので、シミュレーションに組み込むことが容易に可能になります。比熱などのグラフを見れば、滑らかに連続的に変化しているので、回帰式を求めることができると推測されます。グラフの見た目で考えていて数学的にどうかという疑問があるかもしれま延が、ここでは数学的な検証は割愛します。 |
| |
| 最小二乗法で計算した回帰式は次の通りです。 |
| |
 |
| 密度ρ=351.99/T(K) + 344.84/T(K)^2 |
| 粘度μ=1.4592 x 10^(-6) x T^(3/2) / (109.1 + T) |
| 比熱Cp=0.991149-4.910^(-6) x T^(3/2) + 4.68 x 10^(-7) x T^2 ? 1.6 x 10^(-10) x T^3 |
| (ただし、300K以上) |
| 熱伝達率λ= 2.3340 x 10^(-3) x T^(3/2) / (164.54 + T) |
| |
 |
| ● プラントル数の温度依存性 |
| |
| プラントル数=動粘度/熱拡散係数 |
| Pr = ν(m2/s)/α(m2/s) = μ(Pa.s)Cp(J/kgK)/λ(W/kgK) |
| ν=μ/ρ、α=λ/ρCp |
| |
| プラントル数は便利な数値ですが、独立変数ではないので、独立変数が回帰式で表現できればそこから計算できます。 |
| |
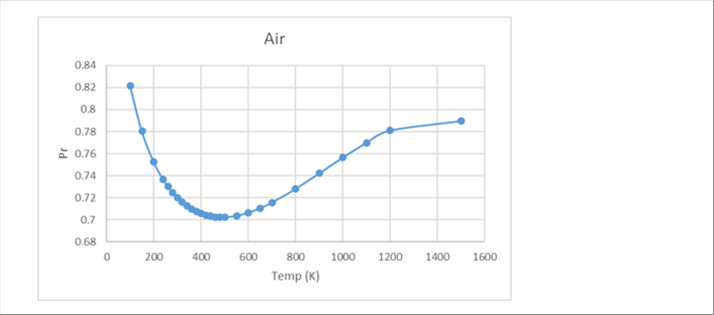 |
| |
 |
| ● 密度、熱拡散係数、粘度の回帰式の評価 |
| |
| 実測値と回帰式を縦軸と横軸にとって相関を見てみると、どれも45度になっていて、よい相関があるといえます。数学的に相関を計算するまでもないと思いますので、数学的な評価は割愛します。 |
| |
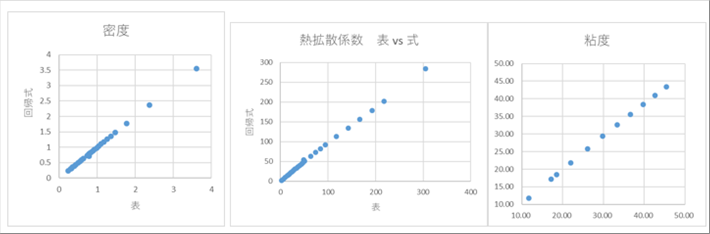 |
| |
 |
| ● 比熱の回帰式の評価 |
| |
| 比熱は独立変数で最重要な数値の一つで、いくるも回帰式が提案されています。グラフにすると次のようになります。 |
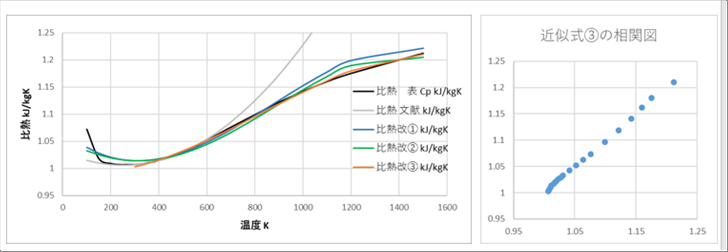 |
| 全温度範囲を一つの式で回帰するのは困難だと思われます。特に、低温での急激な増大を表現するのではむつかしいと思われます。 |
| |
| ただし、この現象は100度Kと低温なので、シミュレーションしたい温度範囲が300度Kより高温であれば、気にする必要はなくなります。 |
| |
| 例えば3番目の回帰式と実際の相関を見れば、実用的な式であることがわかります。 |
| |
| Author: T. Oda |
| このページは、excel2webで自動作成しました。 |































