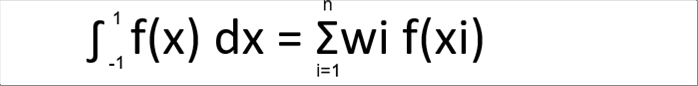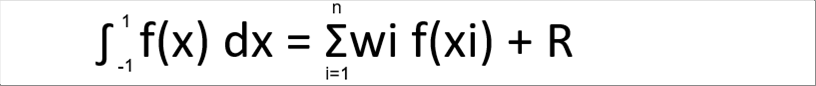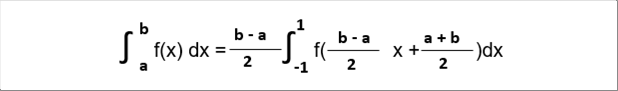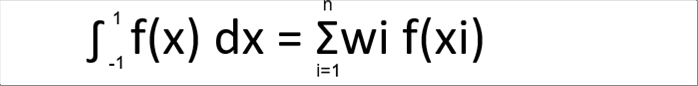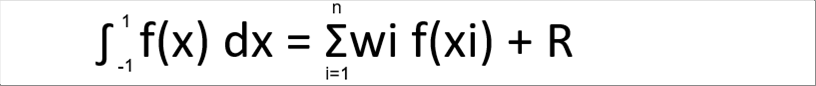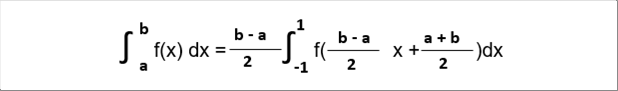Gauss-Legendre Numerical Integration
(1) What is the Numerical Integration?
(2) Gauss - Legendre Numerical Integration
(2)-1 Roots (Representative Positions) and Weight
(2)-2 Calculation Examples
(2)-3 Errors
(3) How to Change the Integration Range
(1) What is the Numerical Integration?
The left side to the differential equations, such as the heat conduction equations and the motion equations of the fluid, is the first-order time derivative. The right side of the equations is the second-order dislocation derivative. Except the very limited case, we cannot solve the equations. The well-known exception is the separation of the variables. We can get the analytical solution; however, the actual equipment are working out of such conditions. Therefore, our great predecessors developed the approximate solutions, such as the finite element method and the difference method. The inevitable errors of the approximation had also been found small enough for the actual utilization. Nowadays, they are widely considered reliable or sufficient for the practical use.
The difference method directly approximates the differential equations by the Taylor expansion. Therefore, no integration is necessary. On the contrary, the finite element method indirectly approximates the differential equations with the mesh generation and the functions inside of the elements. It is necessary to solve the simultaneous equations. It is necessary to integrate the equation during the solving process.
The advantage of the numerical integration is that we can obtain the value even if the formula inside of the elements cannot be integrated. Needless to say, the same process is applicable to the formula, which we can integrate. The numerical integration generates an error; however, we can minimize the error for the practical use.
You will see the Gauss - Legendre numerical integration, which is called Gaussian quadrature as well. We will compare the numerical and integrated solutions in order to know the error is small enough.
(2) Gauss - Legendre Numerical Integration
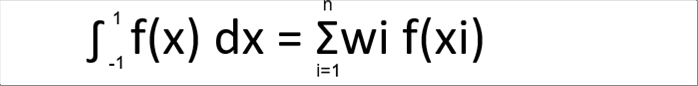The above equation is the Gauss - Legendre formula. Please let me skip how to get it. It clearly shows that we can get the solution even if the f(x) cannot be integrated. We can obtain the solution when we add n numbers of wi times f(xi).
where;
f(x): Function (In the finite element method, it is the equations inside of the elements.)
wi�F Weight
NOTE 1: The integration range is from minus one (-1) to one (1)
NOTE 2: Addtion from one (1) to n.
(2)-1 Roots (Representative Positions) and Weight
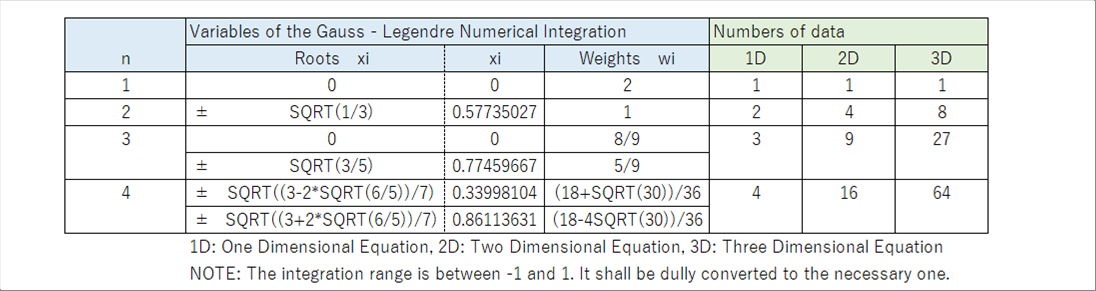
The roots and the weights up to n is four (n=4) are as follows.
The numbers of data increases as the dimension increases, because each numbers of roots for each axis. For example, the number becomes sixty four (64) for the 3D. It is annoying for the manual calculation; however, it actually does not matter for the program.
(2)-2 Calculation Examples
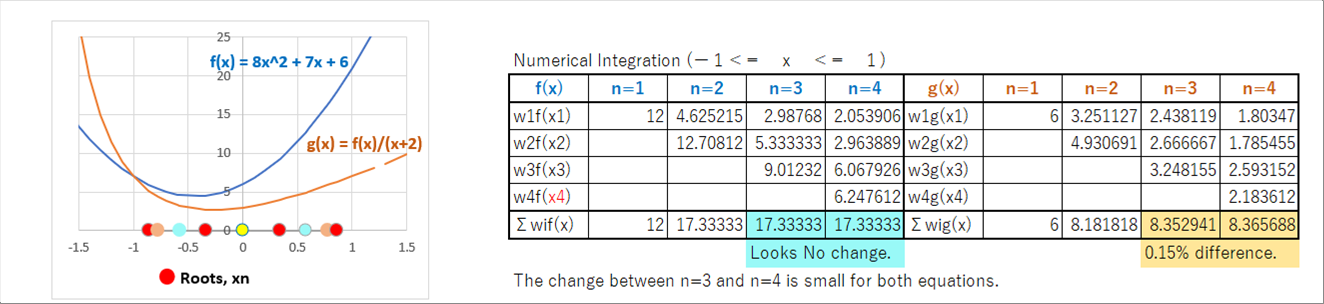
Please find the two (2) examples. One is the simple quadratic function, and another is what is divided by a linear function, which has the singularity. The circles below the graph show the positions of the roots.
The graph shows the two (2) functions. The circles below the graph indicate the roots at n=4. The table indicates the results of the Gauss - Legendre numerical integration. The integral of the functions are available; however, the numerical integration is also available. From the viewpoint of the programming, it may be beneficial to adopt the numerical integration for any functions. (Please see the "Easy Calculus", "Technical Stories" for the basic formula.)
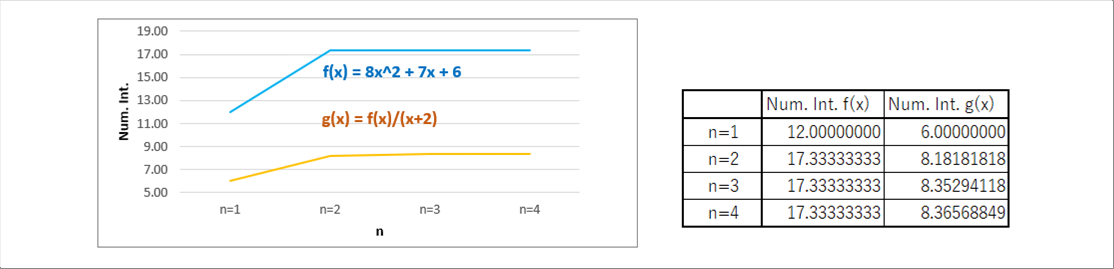
The following graphs shows the variation of the calculated values. Both of them show few changes at N=3 and N=4.
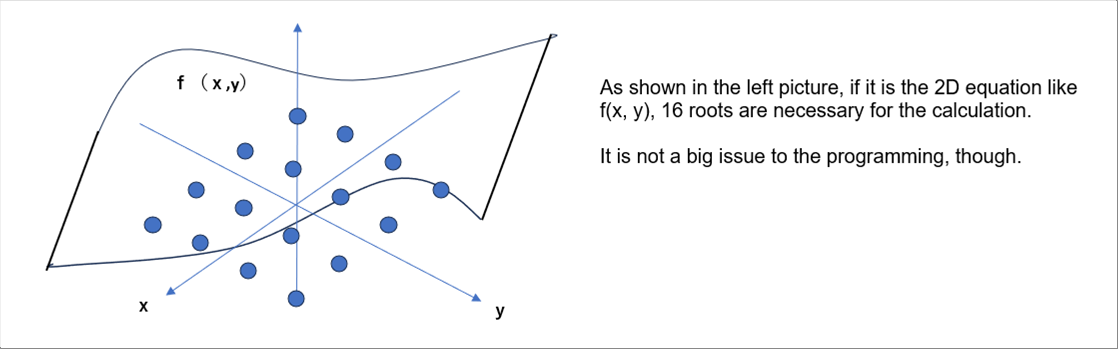
If it is a two-dimensional (2D) function, there are sixteen roots at n=4.
Sixty four (64) roots are necessary for the three-dimensional (3D) ones.
(2)-3 Errors
The Gauss - Legendre equation with the error is as follows.
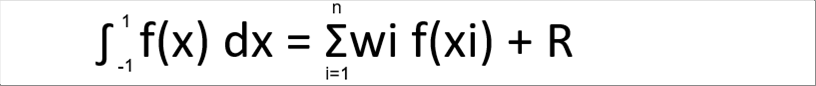The error R is proportional to 2n-th derivative of f (x).
The 2n-th derivative of the (2n-1)-th degree is zero (0). Therefore, if n=4, there will be no error for the equation of the seventh degree or lower. The above example, g(x) = f(x) / (x+2), has a small error even at n=4, though.
For the practical use of the Gauss - Legendre formula, it is advised to calculate n=3 and n=4 in order to be sure if the change between n=3 and n=4 are small enough for your analysis.
In my humble opinion, as long as the f(x) is the quintic (5th-order) equation or less, n=3 should be enough.
(3) How to Change the Integration Range
The range of integration of the Gauss - Legendre formula is between minus one (-1) and one (1). We can change the range by the substitution. (Please see the "Easy Calculus" in the "Technical stories" for the substitution of integration.)
��f(x)dx (interval from a to b)= ��f( g(t) ) dx/dt dt (interval from -1 to 1)
The conditions, "-1<= t <= 1" and "x = g(t) = 0.5 (b-a) t + 0.5(b + a)" satisfy the above equation. The following equation is obatained.
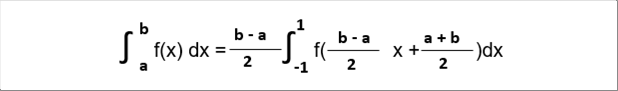Let's substitute the above equation in the Gauss- Legendre formula.
The interval of the integration is converted to from a to b. The error R is omitted, assuming that the n=4.
Author : T. Oda
The page was prepared in Excel, and automatic html and css generation by the "excel2web".