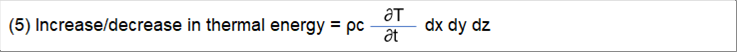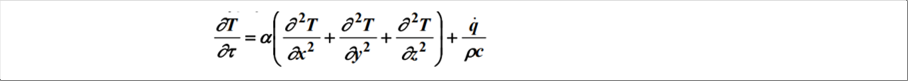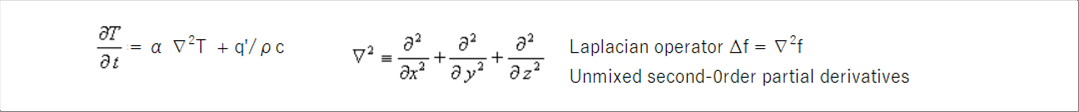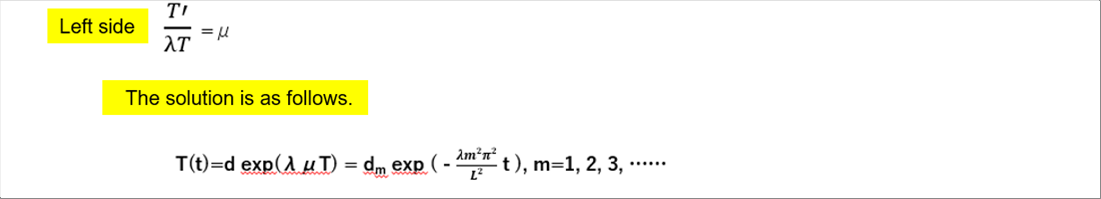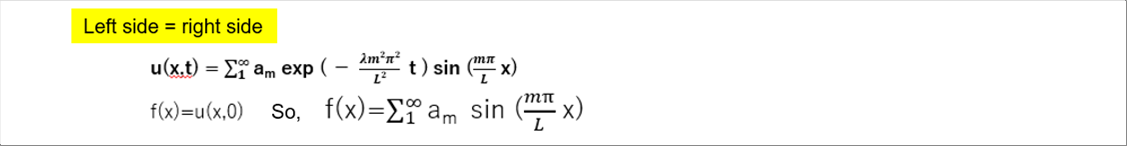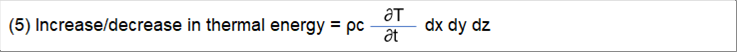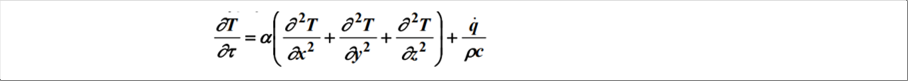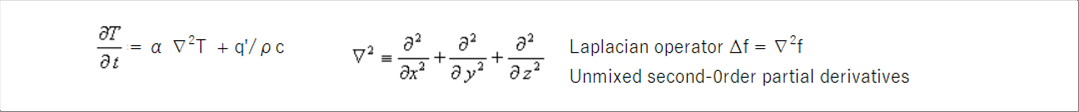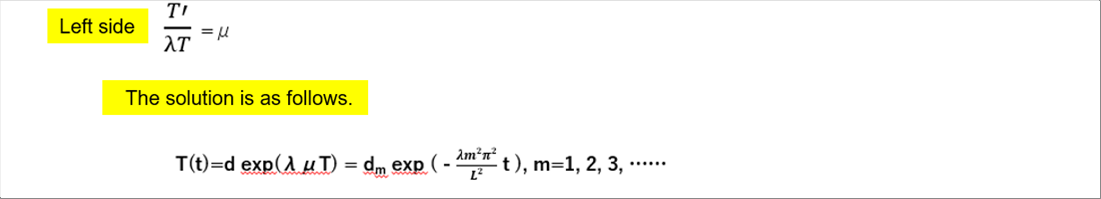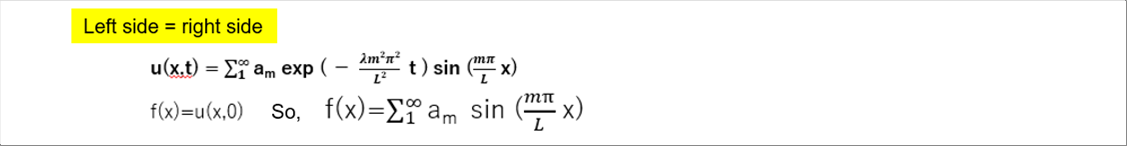| |
 |
| |
 |
| 1 Purposes |
| 2 Fourie's Law |
| 3 Heat Conduction Equation |
| 4 Solution of the Heat Conduction Equation |
| 4-(1) Steps to the Analytical Solution |
| 4-(2) Analytical Solution and Graph |
| |
 |
| 1 Purposes |
| |
| Differential equations such as heat conduction equations and wave equations cannot be solved analytically except in exceptional special cases. Therefore, in practice, numerical calculations such as finite differential method (FDM) are used to perform sequential calculations. The FDM does not provide analytical solutions; therefore errors seems to be a problem. However, since the error is a linear expression of the difference, it has been proven that if the difference is small enough, the ecrus is also small enough. |
| |
| Please see "Easy FDM" for detail. |
| |
| The heat conduction equation can exceptionally be solved if the solution u(x,t) is expressed as the product of the temperature-only equation T(t) and the position-only equation X(x): u(x,t) = T(t)X(x) is famous. The author does not think there are any furnaces that are actually controlled using the formula; however, please let me explain it because it will help you get an idea. |
| |
 |
| 2 Fourie's Law |
| |
| The Fourie's law was introduced as Fourie's cooling law in the story Bais of Thermodynamics, but I would like to introduce it as formula for us to be able to use it in simulations. By the way, Dr. Fourie proposed the formula and solution in the nineteenth (19th) century. |
| |
| In matter, thermal energy is always moving from areas of high temperature to areas of low temperature. |
| |
| The Fourie's law is a formulation of heat transfer. It states that the amount of heat q flowing though a unit area in unit time is proportional to the temperature gradient. Some people may find it difficult to imagine the substance when they hear the term "temperature gradient"; however, it is actually a "temperature difference." The bigger the temperature difference, the bigger the amount of heat flowing. |
| |
| Let's compare the heat of your hand holding the spoon after ten (10) seconds when you dip an aluminum spoon into freshly brewed coffee and when the coffee has cooled down to room temperature after a while. It is hotter when dipped into freshly brewed coffee. This is because the temperature difference between the coffee and the spoon is bigger when you dip the spoon into freshly brewed coffee than when you dip it into cold coffee. |
| |
| Replace the aluminum spoon with a ceramic one. Ceramic spoons are less hot than aluminum ones. This is because ceramic conducts less heat than aluminum. |
| |
| In the way, the way heat is transferred is different depending on the magnitude of the temperature difference. Furthermore, even if the temperature is the same, when the different material is used, there will be a difference in the heat transferring way. The proportionality constant lambda in the case is called heat conductivity. |
| |
 |
| |
| The negative sign indicates the direction of heat movement from a high temperature area to a low temperature one. In real life, the the temperature difference is clear and we do not have to worry about the sign to define the direction of heat transfer. However, when performing temperature simulations, it may not be clear where the high temperature are will be. Then, the sign becomes important. |
| |
| The unit of heat is J, so the unit of 1 is J/J/(sec.m2) = W/m2. The unit of temperature gradient is K/m, so the unit of thermal conductivity lambda is W/m2 / (K/m) = W/(mK). |
| |
 |
| 3 Heat Conduction Equation |
| |
| The heat conduction equation can be obtained form the energy equilibrium in a microscopic volume. Heat and energy are the same thing; however in order to understand them easier, let's consider heat comes in and out, and is generated, while energy accumulates inside. We can write it as follows. |
| |
| Incoming heat + heat generation = increase/decrease in internal energy + outgoing heat |
| |
| (1) Microscopic araa: dx, dy, dz |
| (2) Incoming heat in x direction: qx dy dz (qx:: Incoming heat at position x) |
| (3) Outgoing heat in x direction: qx+dx dy dz (Position x is replaced by x+dx) |
| (4) Heat generation: q' dy dz (q': heat change rate in the microscopic volume) |
| In the motion equation of a body, the time devirative of a body is velosity. The case of heat is similar; the time derivative of temperature is heat (thermal) energy, so we get the following equaiton. |
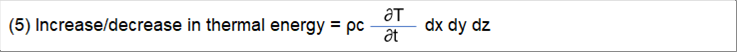 |
| |
 |
| |
| The y and z directions are the same. Therefore, the overall x, y, and z directions are as follows. |
| |
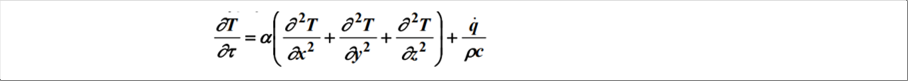 |
| |
| Since the differential equation is long, let's use the nabla operator. |
| |
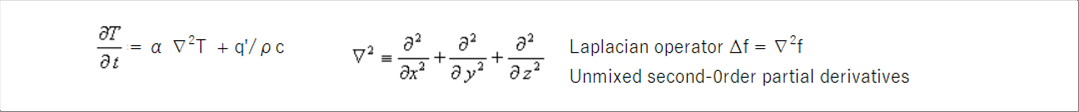 |
| |
 |
| 4 Solution of the Heat Conduction Equation |
| |
| The heat conduction equation is generally unsolvable. A well-known method for solving this problem is called the variable separation method. |
| |
| The steps to obtain an analytical solution to the heat conduction equation, which is derived using Fourie's law, is as follows. |
| |
 |
| 4-(1) Steps to the Analytical Solution |
| |
| (0) In the heat conduction equation is one-dimensional, and heat generation q' = 0. |
| (1) The analytical solution (original function) is assumed to be the product of a only-t function T(t) and a only-x function X(x). |
| (2) Transform the equation so that the right side becomes the equation for T(t) and the left side becomes the equation for X(x). |
| (3) The equation for T(t) and the equation for X(x) are equal only when both of them are same constant. |
| (4) Solve the right and left sides separately. |
| |
| In the one-dimensional heat conduction equation with q'=0, the right side is the second-order differential, and the left side is the first-order differential. As the basis of calculus, trigonometric functions (sin, cos) return to the original expression after being differentiated twice, and exp(x) returns to the original one after being differentiated once. So, we can guess how the steps will be. You get it? (Please see "Easy (Approachable) Calculus" in the "Technical Stories" for detail.) |
| |
 |
| 4-(2) Analytical Solution and Graph |
| |
| Let's follow the steps. |
| |
| From (0) to (3) |
| |
 |
| |
| The right side of (4) is as follows. |
| |
 |
| |
| The left side of (4) is as follows. |
| |
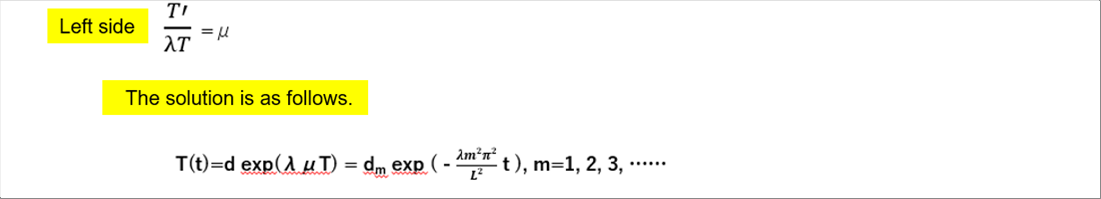 |
| |
| Then, it continues as follows. |
| |
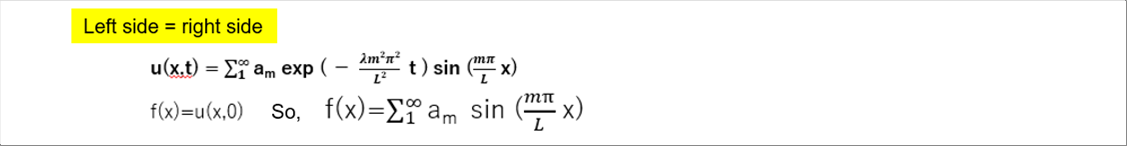 |
| |
| The infinite series sum of only sine in the above equation is called a Fourier sine series. If you are interested, please see the specialized books or websites that explain it. |
| |
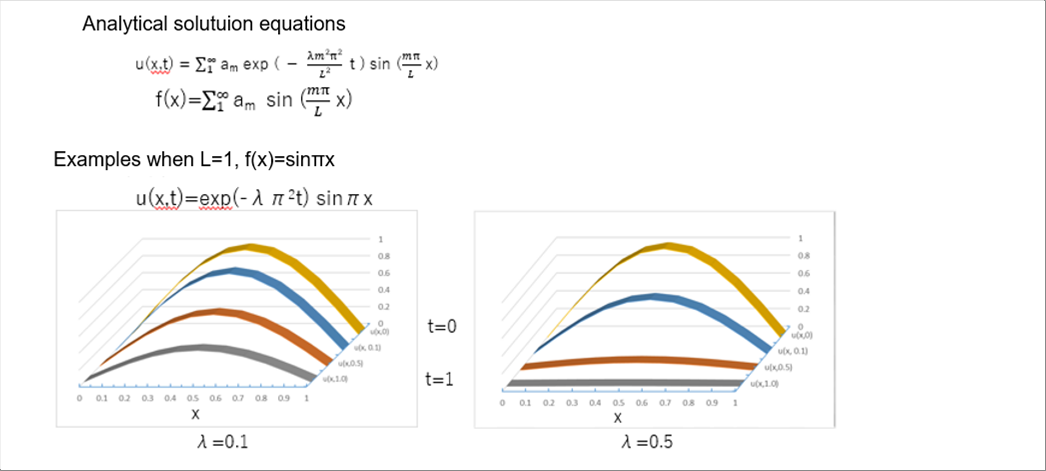 |
| |
| The author does not think anyone will use the results of the analysis to calculate any kind of temperature; however, we can remember the hard works our great predecessors went through in their research in the nineteenth (19th) century, |
| |
| Other thank the past, we can use a laptop to perform three-dimensional simulations that match the actual working environment. Please see the "Numerical Analysis" for detail. |
| |
| Author: T. Oda |
| The page was prepared in Excel, and html and css files were automatically generated by the excel2web. |