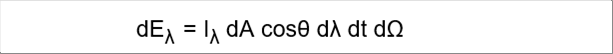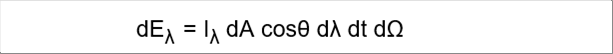Heat Radiation
1 Can Heat be Transferred even in a Vacuum?
2 Brief Summary of Convection and Conduction, Connection with Electromagnetism
2-(1) What Kinds of Substances Emit Electromagnetic Waves?
2-(2) Where do Electromagnetic Waves Go?
3 Radiant Flux and Radiation Shape Factor
4 Calculation of Radiant Energy
5 Energy Radiation Formula of Black Body
5-(1) Radiation Density (radiant flux)
5-(2) Raileigh and Jeans law, Wien's law
5-(3) Planck's Law
5-(4) Stefan-Boltzmann Law
6 Calculation of the Heat Radiation
6-(1) Notes for Simulation
6-(2) Emissivity of Each Material, Temperature, and Surface Condition
1 Can Heat be Transferred even in a Vacuum?
The "Vacuum Insulation Technology" is utilized for the tumblers, the cups and the water bottles. According to the web pages of TIGER, it is clearly explained that "Vacuum, Insulation Technology". It continues that the convection heat transfer can be blocked in a vacuum. Radiation cannot be blocked in a vacuum. They use mirrors in order to reflect the radiation. (I am not sure if there in an English one.) https://www.tiger.jp/b2b/about_dannetsu.html
Heat consists of two (2) types of energy, one is due to the vibration of particles and another is relevant to the wave length of electromagnetic waves. Therefore, heat is a form of energy.
There is no particle in a vacuum, and therefore, the vibration energy does not transfer, but the electromagnetic does. The heat transfer due to the electromagnetic is heat radiation.
2 Brief Summary of Convection and Conduction, Connection with Electromagnetism
- When a material touches another, in addition to radiation, the vibration of the molecules (or atoms) directly transfers. When there is a temperature distribution inside of a material, the vibration transfers inside of the material. The former is convection, the latter is conduction of heat.
- An atom of metal has the same numbers of electrons as the proton. The electrons move freely inside of the metal like gas. Due to the movement of the elections, the heat transfers inside of the metal like gases do as convection. The higher the electrical conductivity of a metal, the higher the thermal conductivity.
2-(1) What Kinds of Substances Emit Electromagnetic Waves?
We tend to think that the smartphones and radio towers emit electromagnetic waves, and carry rice, ramen, and glasses do not. However, everythng emits electromagnetic waves.
It is acceptable that the TV towers and the smartphones emit electromagnetic waves, but it is not easy to accept that the curry rice do as well.
it is hard to believe, but if we take a look at the small particles that form the material. If we drill down the curry rice, it consists of rice, vegetables, meets, curry roux, and water. The majority of all components is water. Therefore, if we consider if the water emits electromagnetic wave, we can consider the rest of the components at the same time.
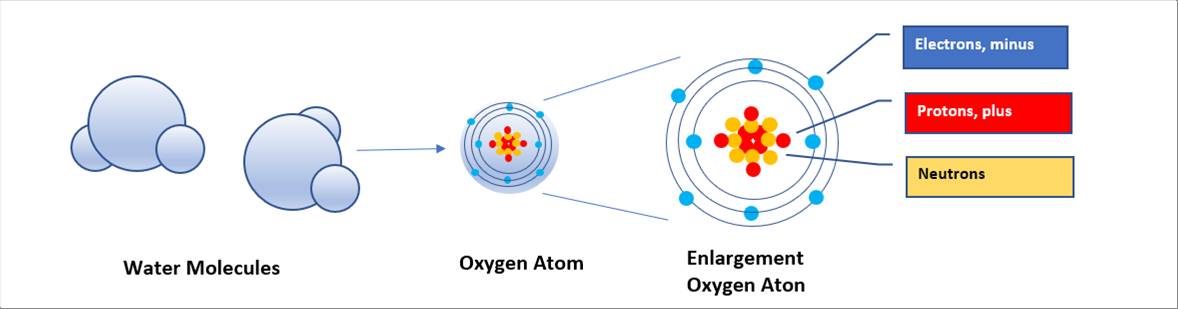
The following pictures show the molecule of water and the atom of oxygen. A molecule of water consists two (2) atoms of hydrogen and an atom of oxygen. Each atom consists of protons, neutrons, and electrons.
The vibration of molecules is heat (energy), and the magnitude of the heat is temperature. Therefore, the molecules of water are vibrating, of which the magnitude meets the temperature. It means both of the atoms of hydrogen and oxygen also are vibrating.
An atom consists of electrons, protons, and neutrons. Protons are positive charge, and electrons negative one. It means that plus and minus are vibrating nearby.
When plus and minus are vibrating nearby, electromagnetic wave is emitted. As a whole, any material with a temperature emits electromagnetic wave corresponding to the temperature. The higher the temperature, the more vibration. Therefore, the higher the temperature of a material, the higher the energy of radiation.
Please let me skip the reason why electromagnetic wave is emitted when plus and minus vibrate nearby, because it is a part of electromagnetism. Please see "near field theory" if you are interested in.
Now, it is clear that the water emits electromagnetic wave. If we follow the other material, we come to the same conclusion. Therefore, curry rice, ramen, glasses and any other materials emit electromagnetic waves.
2-(2) Where do Electromagnetic Waves Go?
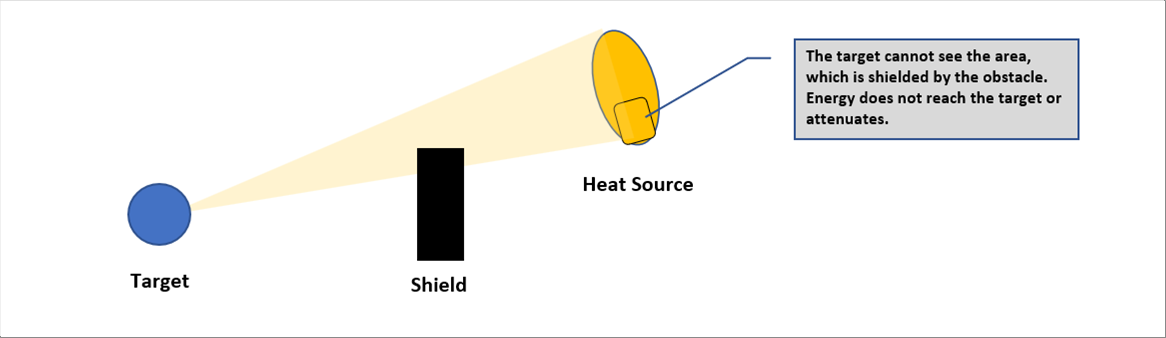
Same as smartphones and TV towers do, any electromagnetic waves emitted by any material go straight to all directions.
It does not reach the target or attenuates by the obstacles.
3 Radiant Flux and Radiation Shape Factor
One of the important points of the radiation is that how much emitted energy can the target receive. It might be due to its importance, it has several terms, such as the radiation density, the radiant lux, or the power flux density.
There is a case that electromagnetic wave reflects off something and reaches the target, and there is a case that the electric wave does not reach the target because it is blocked by an obstacle. The shape radiation factor explains the situation. (Please see the "Shape Factor" for detail.)
4 Calculation of Radiant Energy
Now we know why we have been talking about electromagnetic wave for thermodynamics. Let's continue to the basic equations of electromagnetic waves. It is worth understanding.
The most famous equation is the relationship among wave length, frequency, and light speed. The light speed is constant in a vacuum. Therefore, either the wave length of the frequency is known, we can reduce an unknown value. It is also useful for the integral range conversion. Lastly, we can chose one of them for the horizontal axis of a graph for the easier looking.
Light speed = Wave length x Frequency
The radiant rnergy of black body is obtained by the Integration of radiant rnergy over the entire wave length range and over the entire direction range. It is the famous Stefan Boltzmann Law. "The radiant rnergy is proportional to the fourth power of absolute temperature." The constant of the proportionality is the Stefan Boltzmann coefficient.
The Stefan Boltzmann formula is applicable under ideal conditions.
Ideal conditions: Black body, infinite flat plates. (See "Basis" for the black body.)
The real objects, such as the heating furnaces, reflects some parts of the radiant energy. it has the finite size. Not all walls are flat but leaning. Therefore, it is necessary to consider the emissivity, the surface area, and the coefficient that represents the shape. Let's find the solution by multiplying the radiant energy of a black body by the three(3) terms.
5 Energy Radiation Formula of Black Body
The maximum value of the energy radiation comes from the black body.
- Black body
Black body is the ideal object that perfectly absorb electromagnetic waves of all range of wave length. The black body can emit the biggest radiation at the same temperature. The radiation solely depends on the absolute temperature.
- Electromagnetic field in vacuum
Electromagnetic field in vacuum can be calculated using Maxwell's equations. The outcome is the differential equation for the amount of natural frequency in the minute frequency per unit volume.
- Spectrum
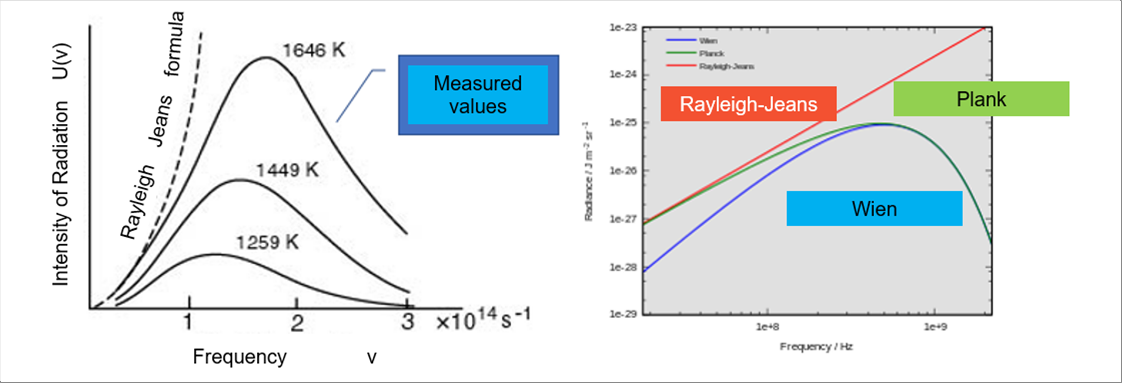
The intensity distribution of each frequency of electromagnetic waves (NOTE: visible light is also electromagnetic waves.) is called the spectrum. The spectrum of a material varies in accordance with the temperature of the material. There are several proposed laws how to express the spectrum. The famous one is the Plank's Law, which consolidates a couple of laws.
- Laws of Radiation Intensity
The Rayleigh-Jeans law matches well at low frequency range, and the Wien law at high frequency range. It is said that the Plank's law fits well in wide range of frequency.
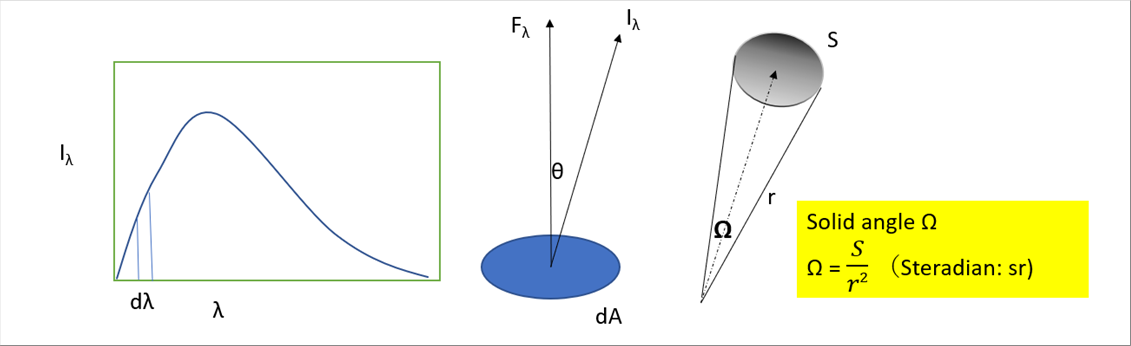
Let's assume that the redation, emitted from the object surface dA, moves to the target at an solid angle. The radiant energy of the small wave length range per small time is defined as follows.
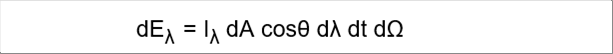The intensity is as follows.
I�� = dE�� / dAcos��d��dt d�� W/m2sr��m
5-(1) Radiation Density (Radiant Flux)
The total radiant intensity is calculated by integrating the radiation intensity over all frequencies.
I = �� I�� d��
The radiation density (radiant flux) is defined as what is in the normal (vertical or radial) direction.
F�� = �� I��
When the radiation density does not change by direction, the total radiation received by the surface perpendicular to the radiation surface is pai times of the density. (The author once forgot multiplying the density by pai, and faced a big difference in the past....)
5-(2) Raileigh and Jeans law, Wien's law
According to the Maxwell's electromagnetisms, the differential equations for the amount of natural frequency in the minute frequency per unit volume is obtained. (Let me skip it in detail.) It is assumed that a certain amount of energy (the degree can be expressed in terms of temperature) is distributed to these natural frequencies. And then, if we know the frequency and intensity of the electromagnetic waves (light is included.) of an object at a certain temperature, we can complete the differential equations. It means that if we measure the spectrum of an object, we get the differential equations.
- Rayleigh and Jeans law
It is only applicable when the frequency is small.
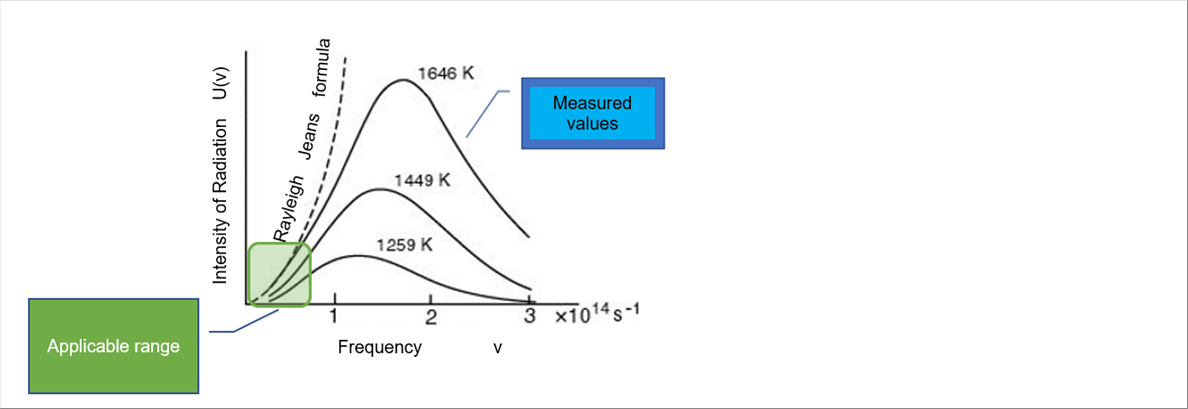- Wien's law
It is assumed that the radiant energy of black body is expressed by temperature, frequency and a function F. When an adequate formula is adopted, the Wien's law holds true (It agrees well with the experimental results.) at high frequencies, but does not hold true at low frequencies.
5-(3) Planck's Law
It is assumed that the function F of the Wien's law as follows.
F(x) = �ȃ� / (exp(��x) - 1 )
He could determine the beta so that it agrees well with the experimental values from the low frequencies to the high frequencies. The numerator of the fraction is expressed as the Planck coefficient, h. (k is the Boltzmann constant.)
h=6.62607 x 10^(-34) Js, k=1.38065 x 10^(-23) J/K
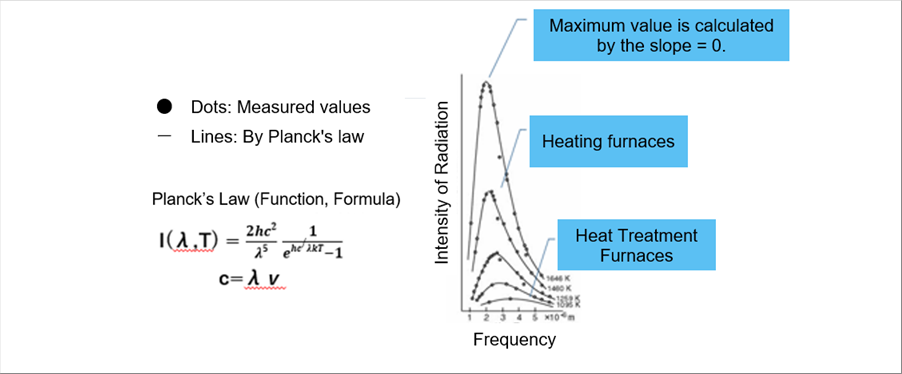I(��,T) = 2hc^2/^5 . 1 / (exp(hc/�Ƀ�T) - 1 )
The important point of the Planck's law is that the radiation intensity is obtained when temperature is defined. It is very convenient for the temperature simulation.
5-(4) Stefan-Boltzmann Law
The total radiation is obtained by the integration of the Plunck's function over the whole frequency range.
The following formula is the Stefan-Boltzmann law.
The outcome is the very famous equation. It says that the total radiation is proportional to the fourth power of absolute temperature.
The radiation density (radiant flux) is as follows. Please do not forget to multiply by pai.
F(T) = ��B(T)
The spectrum pattern is deferent by the temperature, for example, Infrared is dominant at the low frequency range, and ultraviolet is dominant at high frequency range. However, no matter what the spectrum pattern is, the same formula is applicable, because the integration is done over the whole range of frequency.
6 Calculation of the Heat Radiation
The heat radiation of a body is determined by the total radiation multiplied by the emissivity.
6-(1) Notes for Simulation
The heat radiation is proportional to the surface area and the fourth power of absolute temperature. Therefore, it is necessary to pay attention at the higher temperature areas in the heating furnaces. It may be the main source of the temperature simulation in the hot areas. The emissivity should be the actual ones; however, it is sometimes difficult to find the correct number.
6-(2) Emissivity of Each Material, Temperature, and Surface Condition
The manual of the thermometers usually shows tables where you can refer to.
It is strongly suggested to measure the value at the actual applications. Because it shows the wide variation according to the material, temperature, and the surface conditions.
Author: T. Oda
The page was prepared in Excel, and html and css files were automatically generated by the excel2web.