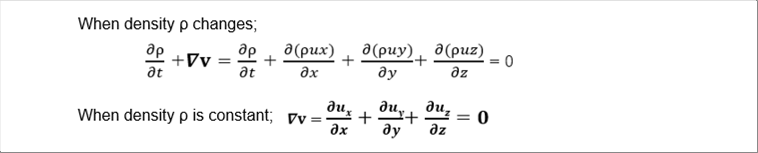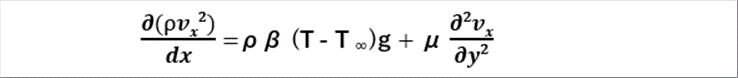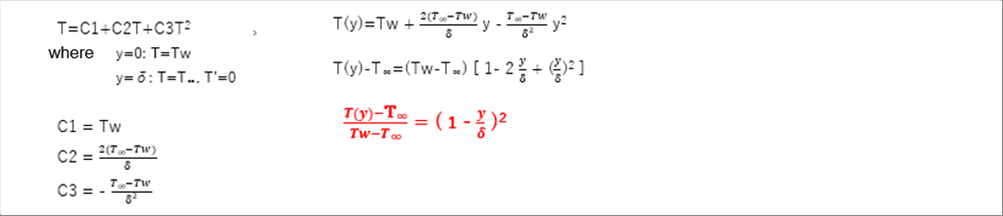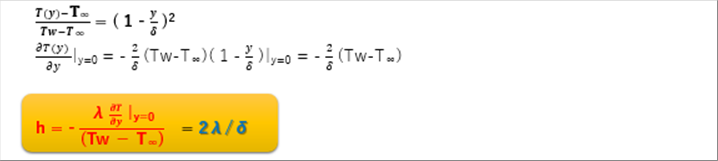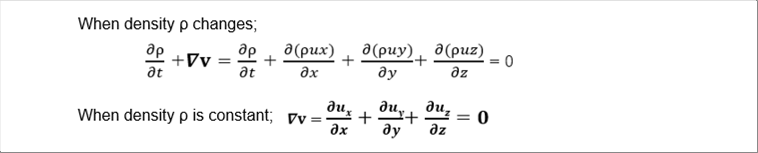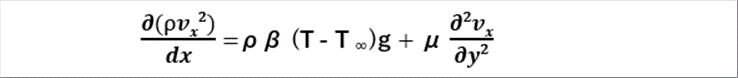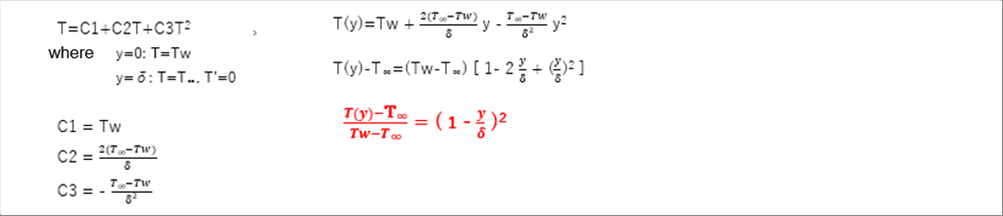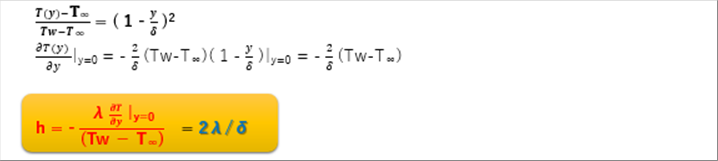| |
 |
| |
 |
| 1 Natural Convection Heat Transfer Coefficient (Round Steel Billet) |
| 2 Natural Convection and Forced Convection |
| 3 Analysis of Natural Convection |
| 3-(1) Experimental Formula for Convection Heat Transfer Coefficient |
| 4 Range of Flow to know Convection Heat Transfer Amount |
| 4-(1) Overview of Equations Applied Within the Boundary Layer |
| 4-(2) Equation of Convection Heat Transfer Coefficient = 2 x Thermal Conductivity / Boundary Layer Thickness |
| 5 Navier-Stokes Equation and Continuity Equation for Incompressible Fluids |
| 5-(1) Navier-Stokes Equation |
| 5-(2) Equation of Continuity |
| 6 Velocity Boundary Layer |
| 7 Temperature Boundary Layer |
| 8 Relationship between Prandtl Number and Velocity/Temperature Boundary Layers |
| 8-(1) Prandtl Number |
| 9 Assumption of Velocity Distribution |
| 10 Navier-Stokes Equation within Boundary Layer |
| 11 Calculation of Velocity Distribution |
| 12 Energy Equation within Boundary Layer |
| 13 Calculation of Temperature Distribution within Boundary Layer |
| 14 Calculation of Convection Heat Transfer Coefficient |
| 15 Navier-Stokes Integral Equation in the Boundary Layer |
| 16 Boundary Layer Thickness and Velocity Equation |
| 16-(1) Thermal Energy Integral Equation in the Boundary Layer |
| 16-(2) Determine the Boundary Layer Thickness |
| 17 Prandtl Number Pr, Grashof Number Gr, Nusselt Number Nu, Boundary Layer Thickness |
| 18 Heat Transfer Coefficient of Natural Convection h, Function of Position |
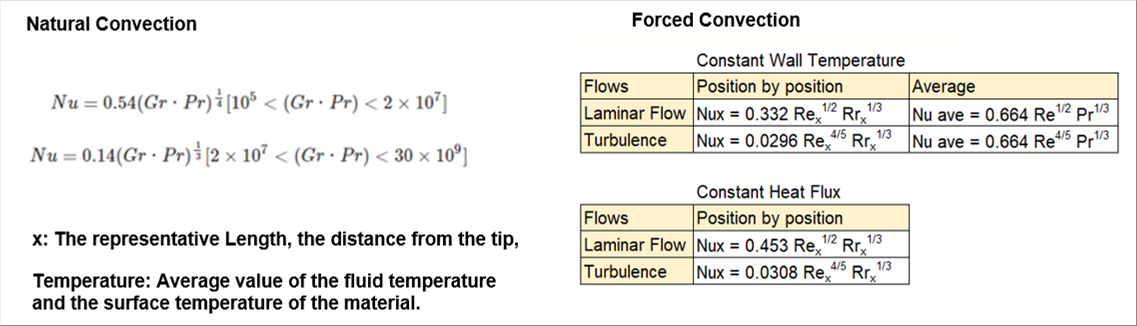
| 19 Forced Convection Heat Transfer, Experimental Formula for Nusselt Number |
| |
 |
| 1 Natural Convection Heat Transfer Coefficient (Round Steel Billet) |
| |
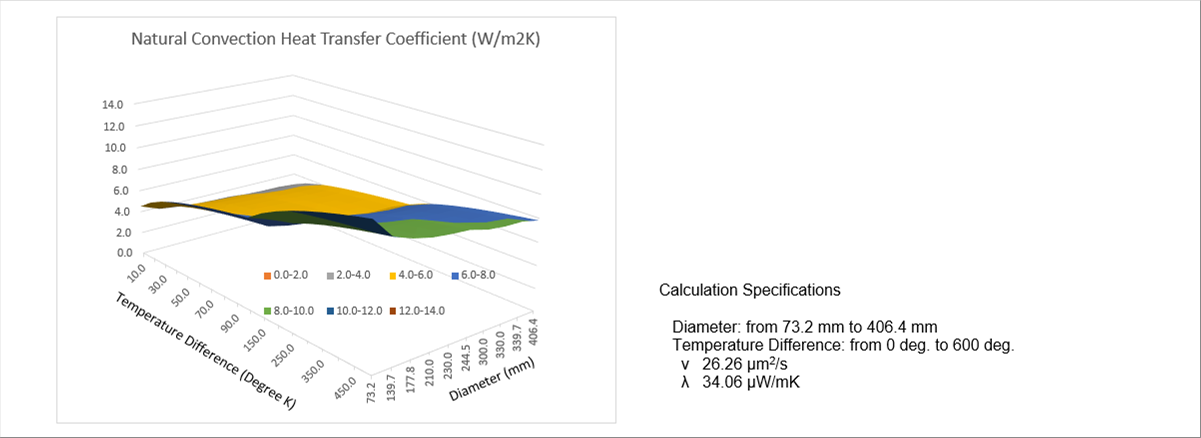
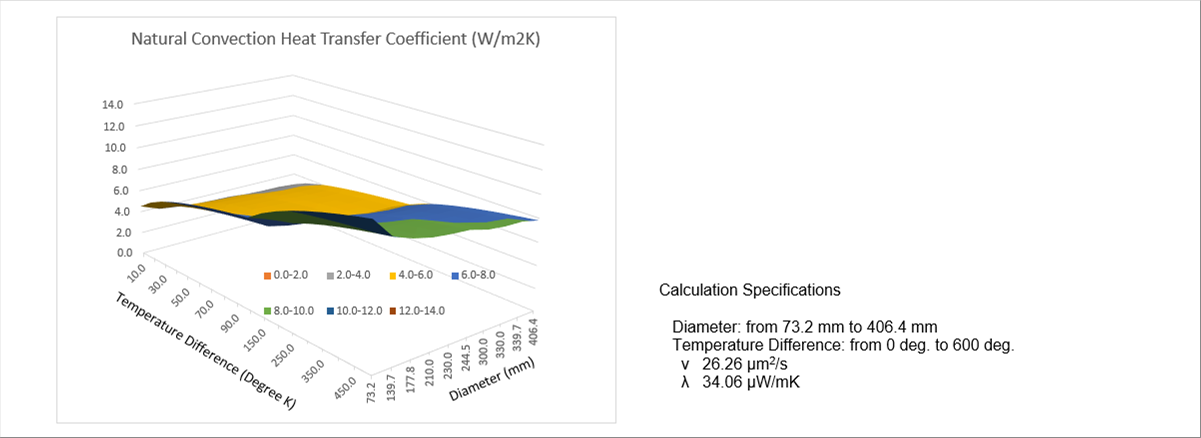
| The following graph shows the calculated results of a round steel billet. Outside diameter: from seventy three (73) mm to four hundred and six point four (406.4) mm, temperature difference: from zero (0) degree to six hundred (600) degrees. The calculated narural convection heat transfer coefficint is about six (6) W/m2K. |
| |
| According to the author's experience, it looks similar to the reality. There will be several ways how to utilize the coefficient in the temperature simulation. I have summarized the basic concept and calculation method. |
| |
 |
| |
 |
| 2 Natural Convection and Forced Convection |
| |
| Let's think about how things cool down when placed the following conditions. |
| |
 |
| |
| The environment where the things placed is in a vacuum, liquid, or air. Let's concentrate on the liquid and on the air because we will see the convection. |
| |
| One cold example is that when dry ice is places in a sink, white smoke spreads to the bottom of the sink. One hot example is that the sparks fly up in a campfire. Even if there is no wind, both of the white smoke and the sparks flow naturally just being there. |
| |
| The reason why they move is due to the temperature difference from the surrounding air. If the temperature difference exists, heat transfers from hot area to the cold area. The heat of the hot surrounding air transfers to the cold dry ice. The heat of the fire transfers from the campfire to the cold surrounding air. Similar to the campfire, when a hot steel or iron is placed in air, the heat transfers from the hot steel to the cold air. In any case, the temperature difference gradually decreases. |
| |
| When there is no wind, air velocity can be considered zero; however, the phenomenon still occurs. This is called cooling (heating) natural convection. As the velocity of flued increases, heat transfer due to convection increases, which is called forced convection. Please note that like a falling meteorite, if the velocity is too high, friction between the air and the object and adiabatic compression of air generate heat, and hence increasing the temperature of both. |
| |
| In rotary hearth heating furnaces, walking beam heat treatment furnaces, etc. that to-be-heated materials, there is a flow of combustion gas, so, we can say that it is forced convection. But there is a temperature difference between the combustion gas and the to-be-heated materials such as round steel billet, pipes, plates, etc. Natural convection is also occurring. Therefore, it is necessary to consider both. Since the materials are placed at the bottom of the furnace, the combustion gas velocity here is lower than the average velocity, and in some cases, forced convection may be so small that it can be ignored. Therefore, here, let's consider heat transfer by natural convection. |
| |
 |
| 3 Analysis of Natural Convection |
| |
| The basic equations used in the analysis are the Navier-Stokes equation, which is the fluid motion equation, and the thermal energy equation. Both are second-order differential equations. of the equations. If we can create as many equations as the variables, we will get a solution. In addition to the known temperature distribution of the initial state, we can also use the integral equation obtained by integrating the second-order differential equation once. Therefore, it is highly likely that we can create equations with the same number of variables. |
| |
| Let's treat the gas as incompressible. In reality, gas is compressive, but if the density change is up to five precent (5%), they say that it is safe to treat it as incompressible. The limit number is Mach zero point three (0.3) or less, so if the gas velocity is ninety nine point four five (99.45) m/s, which is two hundred and twenty two (222) mph, or less, it can be treated as incompressible. |
| |
 |
| 3-(1) Experimental Formula for Convection Heat Transfer Coefficient |
| |
| Many experimental formula have been reported for the heat transfer coefficient of natural convection. For example, according to the Meiji University's website, it is classified by heating or cooling, material is either on top of or bottom, etc. |
| |
| For operation, it is enough if you can use them. However, it seams meaningful to understand the meanings of numbers and their reasons used in the experimental formula such as Reynolds number Re, Prandtl number Pr, Rayleigh number Ra, Nusselt number Nu, etc. It is useful to understand why the Nusselt number Nu multiplied by the thermal conductivity (a physical property value, which is temperature dependent) and divided by distance comes to the heat transfer coefficient. |
| |
 |
| |
| |
 |
| 4 Range of Flow to know Convection Heat Transfer Amount |
| |
| The amount of heat transfer by natural convection is affected by flow velocity, density, convection heat transfer coefficient. However, it is not necessary to analyze the entire flow, but it seams sufficient to understand the flow around the material. |
| |
| The velocity distribution of the fluid around a material is such that the velocity on the material's surface is zero (0), gradually increases as it travels away from the material, and reached a constant value when it is far enough away. The region where the velocity changes is the velocity boundary layer.. Please see "Fluid Mechanics" for more information. |
| |
| Similarly, the temperature of the fluid is also changing. Fluid temperature on the surface of a material is same as the material temperature, gradually changes as it moves away from the material, and reached a constant (fluid temperature) value when it is far enough away. The region where the temperature changes is the temperature boundary layer. Please not that the velocity boundary layer and the temperature boundary layer are not necessarily same. |
| |
 |
| 4-(1) Overview of Equations Applied Within the Boundary Layer |
| |
| - Equations |
| |
| The Navie-Stokes equations, which are equations of motion for fluids, and the thermal energy equations also hold true within these boundary layers. However, it is very difficult to solve these equations analytically (they cannot be solved except very special case), so the conditions should be simplified to the extent that there are no (little) engineering problems. |
| |
| - Treatment of Natural Convection |
| |
| In natural convection, the external force term in the Navier-Stokes equations is buoyancy, which creates velocity in the fluid. Thermal energy moves from a high temperature area to a low temperature area where a fluid and a material come into contact. The amount of the thermal energy from the hot area to the cool area is the amount of heat transfer of natural convection. |
| |
| - Thermal Dependence of Physical Properties of Air (See "Temperature Dependence of Air" for more information) |
| |
| In many heating furnaces and heat treatment furnaces, the fluid is often air (combustion gas). Air density, viscosity, heat transfer coefficient, etc. depend on temperature, therefore, it is necessary to use the appropriate values. |
| |
 |
| 4-(2) Equation of Convection Heat Transfer Coefficient = 2 x Thermal Conductivity / Boundary Layer Thickness |
| |
 |
| |
| The above equation says that if we know the temperature gradient on the surface of a material, we can calculate the convection heat transfer coefficient. In order to find the temperature gradient on the surface of the material, it is necessary to solve the simultaneous equations of the Navier-Stoke equation (fluid motion equation) in the velocity boundary layer and the thermal energy equation in the temperature boundary layer. The solution is that Convection heat transfer coefficient is twice the thermal conductivity divided by the thickness of the boundary layer. |
| |
| The conclusion is enough for the temperature simulation. We will follow the calculation path to conclusion for deep understanding. |
| |
 |
| 5 Navier-Stokes Equation and Continuity Equation for Incompressible Fluids |
| |
| The motion of fluid are affected by many items such as density, inflow, outflow, viscosity, internal pressure, external force, etc. The Navie-Stokes equation express the relatinship among them. |
| |
| The Navier-Stokes equation is three-dimensional equation of motion, and therefore, it becomes very long if we write in each axis. We will see the similar expressions many times and the author's typo as well. |
| |
| Some people might have never seen it before; however, the Nabla operator and Laplacian operator are convenient in situations like this. We see the short equation. Another benefit is that the equation will be the same regardless coordinate systems. The representation remains same in Cartesian and polar coordinate systems. |
| |
 |
| 5-(1) Navier-Stokes Equation |
 |
| |
| The above equation shows that the velocity of the fluid, which changes at location r and time t, is determined by the pressure p applied to the fluid, the fluid velocosity, and the external force f. |
| |
| Nabla and Laplacians are operators that are often seen when we look for equations of physical phenomena in mathematical formulas. The author think that they have an advantage in terms of ease of viewing the formula compared to notation in the Cartesian coordinate system, for example. |
| |
 |
| 5-(2) Equation of Continuity |
| |
| The equation of continuity when the density and the velosity of the material change is as follow. |
| |
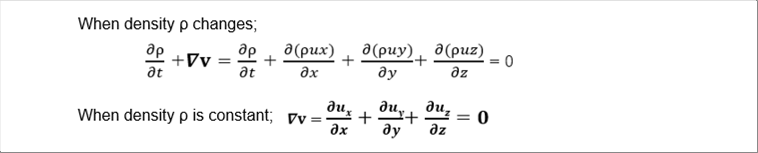 |
| |
| The fact that fluid is continuous means that when it gathers, its density increases, and when it goes out, its density decreases. It means that the fluid won't break and no vacuum space is created. The Navier-Stokes equation is complex because it is a second-order differential equation. On the contrary, the equation of continuity is very simple because is it first-order one. We do not need Nabla operator, but the equation in the expression in Cardician coordinate system is easy to see. |
| |
| |
 |
| 6 Velocity Boundary Layer |
| |
| When a fluid flows aound a material, the viscosity of the fluid creates a "velocity boudary layer", and area of low velocity near the surface of the material. The velosity is zero (0) at the material's surface and the velosity is ninety nine percent (99%) at the boundaty. At a sufficient dintance from the meterial, it becomes the velocity of the flow. |
| |
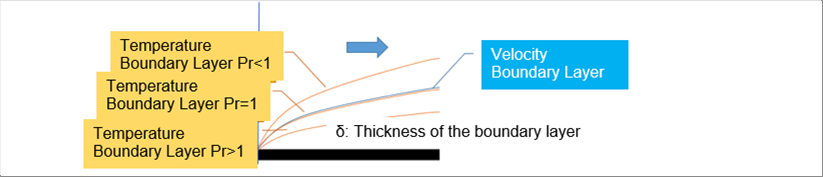
| The first question of flow is whether the flow is laminar or turbulent. The velocity boundary layer also show different aspects between laminar flow or turbulent flow. We are considering the case of natural convection here, let's look at the case of laminar flow. Please take a look at the following picture (same one above) again. There are three (3) temperature boundary layers (red lines) for one velocity boundary layer (black line). |
| |
 |
| |
| |
 |
| 7 Temperature Boundary Layer |
| |
| The temperature boundary layer becomes thinner when the fluid velocity is fast and thicker when the fluid viscosity is big. The temperature of the fluid at the surface of a material is the material temperature, and the temperature changes as the position is far from the material. it becomes the flow temperature at a sufficient distance from the material. The temperature of the material may be higher or lower than that of the fluid, therefore, the temperature distribution within the temperature boundary layer does not necessarily match the velocity distribution within the velocity boundary layer. |
| |
| |
 |
| 8 Relationship between Prandtl Number and Velocity/Temperature Boundary Layers |
| |
 |
| |
| A dimensionless number called the Prandtl number is used as an index of the relationship between the thickness of the velocity boundary layer and the temperature boundary layer. Please let me skip the rest of the indexes that are used in the same purpose. |
| |
 |
| 8-(1) Prandtl Number |
| |
 |
| |
 |
| |
| As the density and kinetic viscosity of air change greatly depending on the temperature, the author drew a graph of the Prandtl number as above. The Prandtl number for the temperature range of air for the practical use in the plant shoo floors are three hundred (300) degrees K and higher is less than one (1). Therefore, the thickness of the temperature boundary layer of air is likely being thinner than the velocity boundary layer. |
| |
| |
 |
| 9 Assumption of Velocity Distribution |
| |
 |
| |
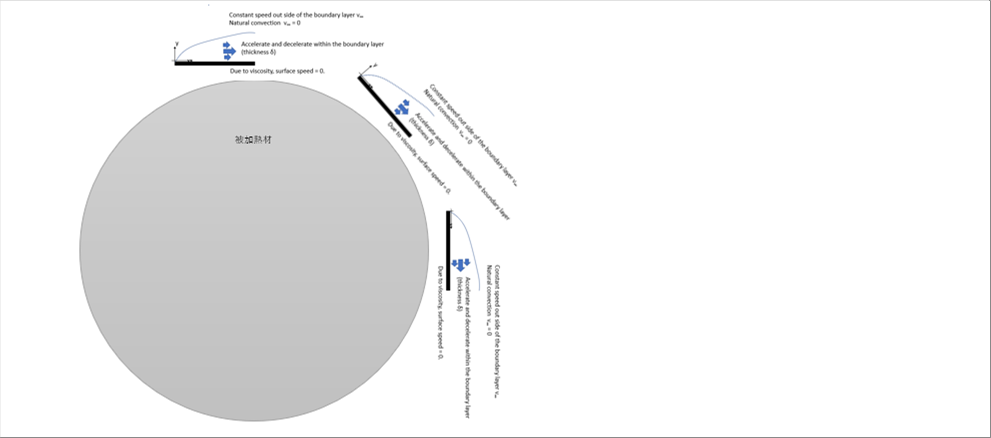
| If we consider the case of a material with a round cross section, it can be expanded to the case of a quadrilateral cross section. |
| |
| Considering the three cases of top, right middle, and side, it can be referred that the flow is similar, although the boudary layer thicknesses are different. That is, within the velocity boundary layer, the velocity of the fluid at the surface is zero (0) due to viscosity, increases and decreases within the boundary layer, and returns to zero (0). |
| |
| The dominant velocity component changes depending on the location. On the top of the material, vx is dominant, and on the side, vy is dominant, and right middle seems being the same for both. In any case, the speed is zero when the distance is far enough away from the surface. |
| |
| Therefore, since velocity has two inflection points, a cubic equation for position seems appropriate. (Four boundary conditions are necessary.) |
| |
| |
 |
| 10 Navier-Stokes Equation within Boundary Layer |
| |
| We need the Navier-Stokes equation in the boundary layer in order to calculate the convection heat transfer coefficient. The direction x perpendicular to the screen surface is the length direction of the material. The z-axis should also be included in the three-dimensional analysis; however, in order to simplify the calculation, let's assume that there is no clow in the z-axis direction. |
| |
 |
| |
| Let's proceed with calculations utilizing the techniques often used when expanding calculus equations. (See Basis of Calculus for detail.) |
| |
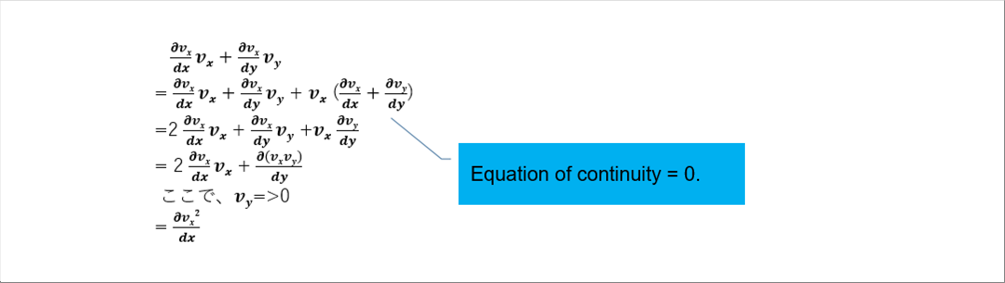 |
| The inside terms in the blankets ( ) comes to the second derivative of x-direction velocity. |
| |
| The Navier-Stokes equation in the boundary layer is defined by: |
| |
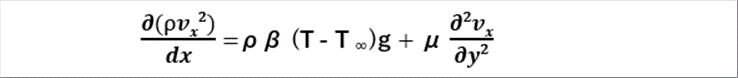 |
| |
 |
| 11 Calculation of Velocity Distribution |
| |
| We have obtained the motion equation within the boundary layer. Let's solve it in order to know the thickness of the boundary layer. |
| |
 |
| |
| The velocity vx at position x in the boundary layer varies along the y-axis. As we assumed before stating the calculation, it is assumed appropriate to express the velocity by an approximate curve with two inflection points. |
| |
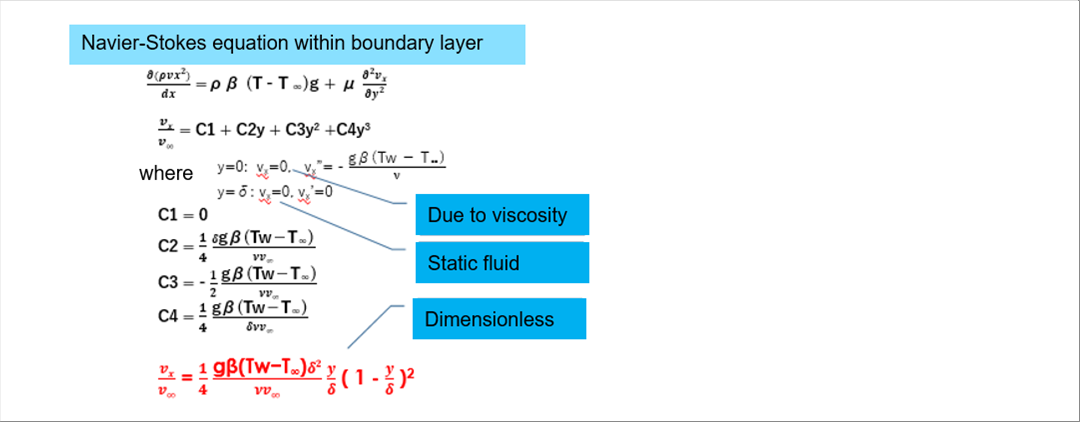
| By creating a cubic equation using the ratio of vx and fluid velocity, the above conditions can be satisfied at the same time. Let's identify the constant terms of the cubic equation. |
| |
 |
| |
| The parts that says "where" is the boundary conditions for the identification of the constnts. The contents explained above the formula is used. |
| |
| (1) The velocity vx=0 at the material's surface due to viscosity. |
| (2) Enter the condition (1) in to the equation for the velocity rate on the material's surface y=0 . |
| (3) The velocity on the boundary layer = 0. |
| (4) Velocity rate on (and out of) the boundary layer = 0. |
| |
| Since there are four unknows and four boundary conditions, the constant terms of the cubic equation can be determined. |
| |
 |
| 12 Energy Equation within Boundary Layer |
| |
 |
| |
 |
| 13 Calculation of Temperature Distribution within Boundary Layer |
| |
| The fluid temperature on the material's surface is the material's temperature. From there, the fluid temperature changes rapidly to the fluid temperature at the boundary. Since there is one inflection point, it can be approximated by a quadratic equation. |
| |
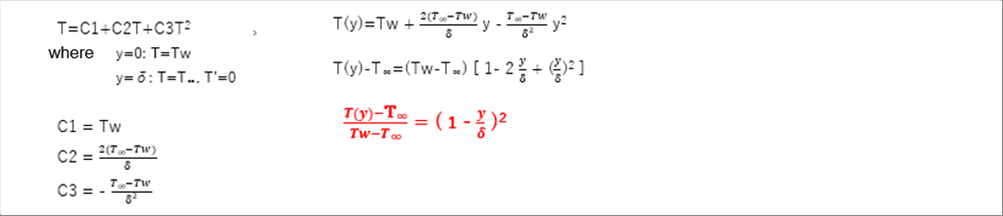 |
| |
| |
 |
| 14 Calculation of Convection Heat Transfer Coefficient |
| |
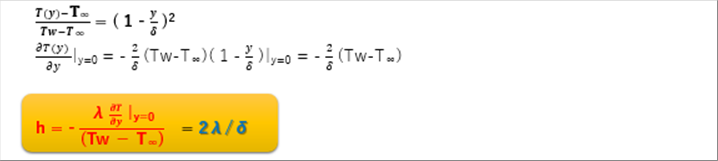 |
| |
| By submitting the temperature gradient of the material surface y=0 in to the formula for the convection heat transfer coefficient, we obtain the coefficient as follows. |
| |
| Convection heat transfer coefficient h = 2 heat conductivity / Thickness of the boundary layer |
| |
| The thickness of the boundary layer is obtained by the Navier-Stokes equation within the boundary layer. We will follow the calculation sequence as seen in the Contents. The author is afraid that even if you are a patient person who has read this far, you may feel discouraged if you think that there is still a long way to go. In order to encourage you, please find the outcome in advance. The author believe that you can also guess how the complicated coefficients of Prandtl number, Grashof number, and Nusselt number were determined. |
| |
 |
| |
| |
| |
 |
| 15 Navier-Stokes Integral Equation in the Boundary Layer |
| |
 |
| |
 |
| |
| |
 |
| 16 Boundary Layer Thickness and Velocity Equation |
| |
 |
| |
| |
| |
 |
| 16-(1) Thermal Energy Integral Equation in the Boundary Layer |
| |
 |
| |
 |
| |
 |
| 16-(2) Determine the Boundary Layer Thickness |
| |
| We can summarize all the above discussion as follows. |
| |
 |
| |
 |
| 17 Prandtl Number Pr, Grashof Number Gr, Nusselt Number Nu, Boundary Layer Thickness |
| |
| Prandtl number, Grashof number, and Nusselt numbers are proposed as follows. These numbers are used when organizing experimental formulas under various heating and cooling conditions. |
| |
 |
| |
| All the variables are known. Some are physical property values, g is gravitational acceleration, some are boundary conditions, and x is the position you want to know. All of the numbers are the functions of x |
| |
| Therefore, the dimensionless boundary layer thickness is as follows. |
| |
 |
| ? �� / x = 3.936 Gr^( -0.25) x Pr ^ (-0.5) x ( 0.952 + Pr )^0.25 |
| |
 |
| 18 Heat Transfer Coefficient of Natural Convection h, Function of Position |
| |
| By submitting the boundary layer thickness determined in the previous section into the formula of the convection heat transfer coefficient h, h can be calculated as follows. |
| |
 |
| |
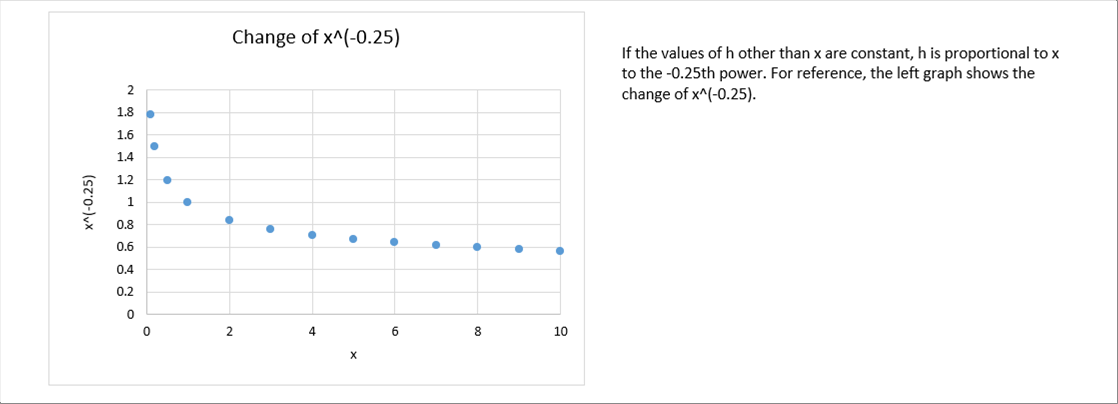
| Both of Prandtl number and Grashof number depend on temperature, velocity, etc., it is difficult to imagine how h will change. In order to assume changes in h, let's consider a case where the temperature, velocity, etc., are constant. In the case, we can see that h is proportional to x to the -0.25 power. |
| |
 |
| |
| The convection heat transfer coefficient h is the maximum at the point where the fluid comes to contact with the material and begins to move (float) due to buoyancy, and decreases as it travels away from the material. |
| |
| The first graph of the page uses the formula to calculate the natural convection heat transfer coefficient, which varies temperature and size of the round billet. |
| |
 |
| |
 |
| 19 Forced Convection Heat Transfer, Experimental Formula for Nusselt Number |
| |
| In the previous section, the heat transfer coefficient of naturaul convection was obtained as the flow velocity is zero (0). If the velociis small, it should be ok in calculating natural convection; however, if the velocity is large to some extent, then forced convection should be necessary. If you use a laptop, we can follow the same method as in the previous section. |
| |
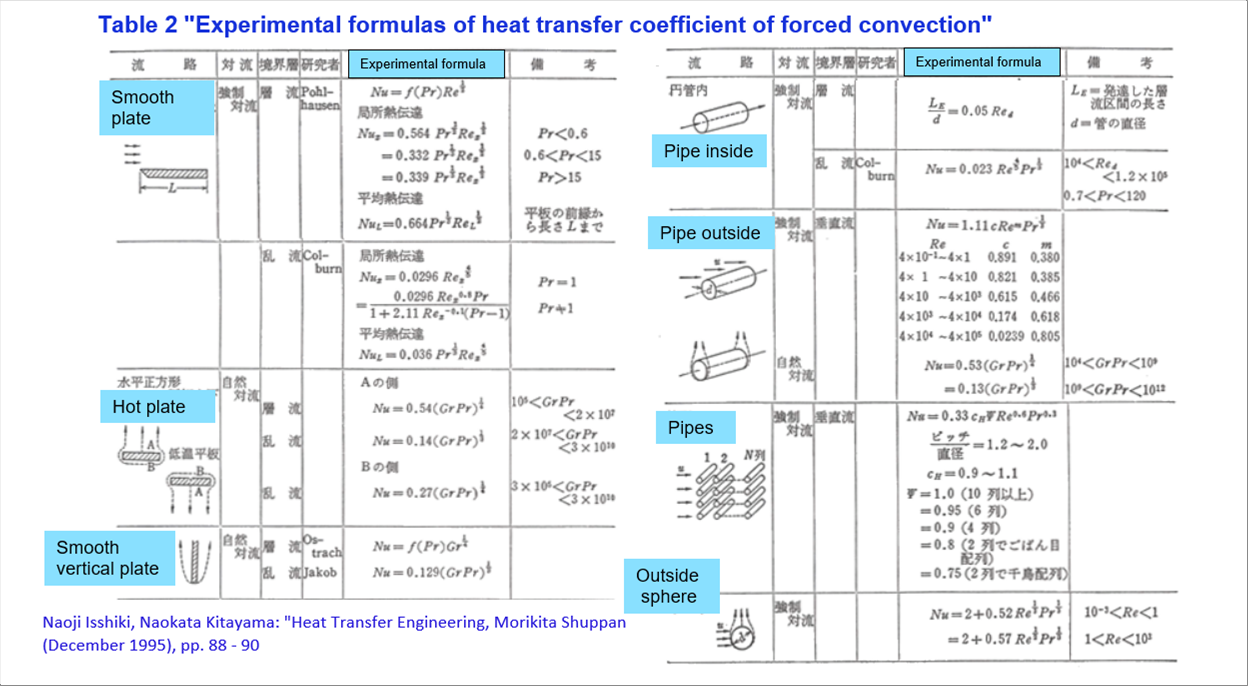
| If the Nusselt number is known, it is easy to obtain the heat transfer coefficient of forced convection. It is so useful that experimental equations have been proposed, for example, the coefficients C and m at Nu=C(GrPr)m. In the days when there were no computers, it might have been the only option; however, it can still withstand practical use today. |
| |
| The website "Atomic Energy Encyclopedia ATOMICA" introduces experimental formulas for some conditions in Table 2 "Experimental formulas of heat transfer coefficient of forced convection". According to the website, the source is Naoji Isshiki, Naokata Kitayama: "Heat Transfer Engineering, Morikita Shuppan (December 1995), pp. 88 - 90. |
| |
| There is also experimental formulas using the Rayleigh number Ra=GrPr. What is proposed is the same. |
| |
| In any case, our seniors are great. |
| |
| The followint table shows an example of Nu=C(GrPr)m, then calculate C and ��, |
| |
 |
| |
| |
| Author: T. Oda |
| The page was prepared in Excel, and html and css files were automatically generated by the excel2web. |