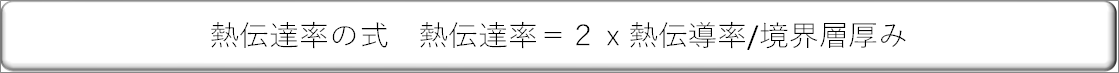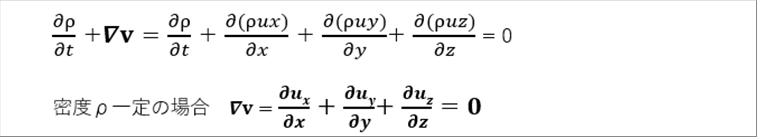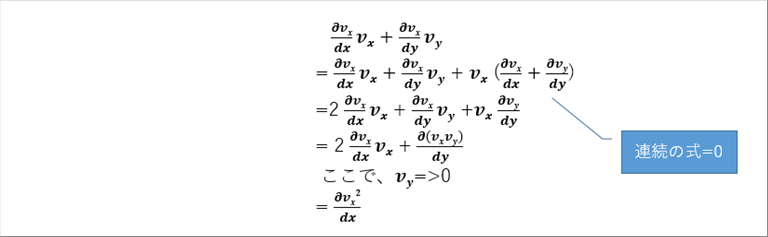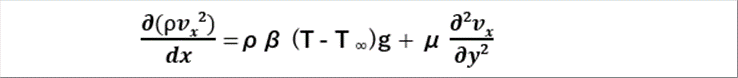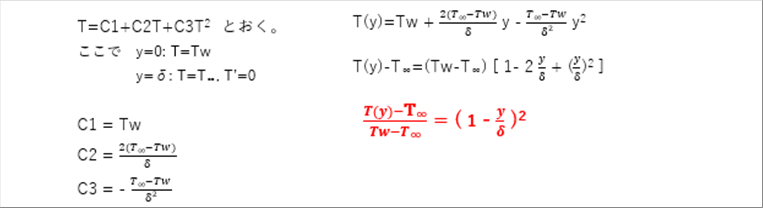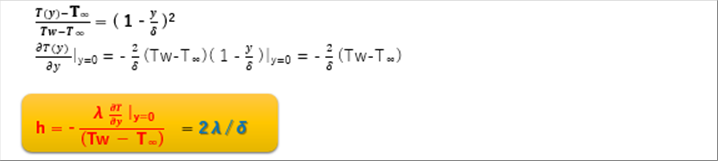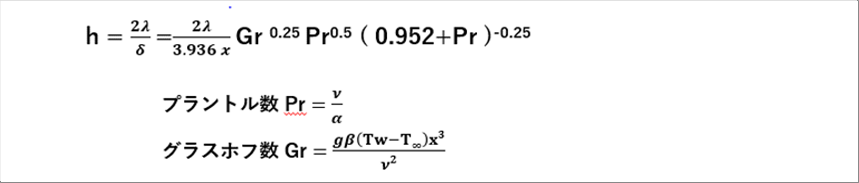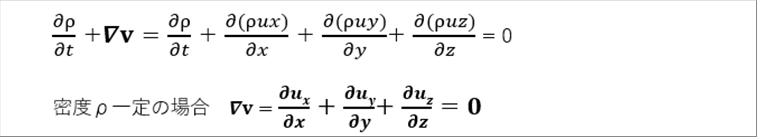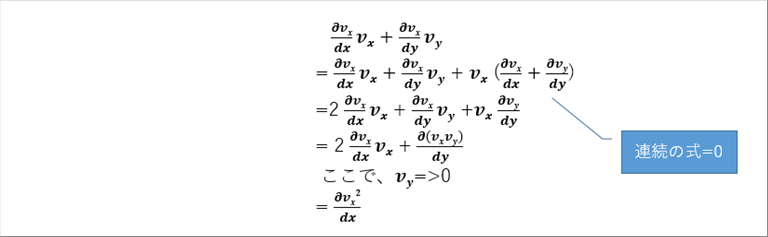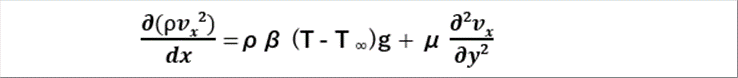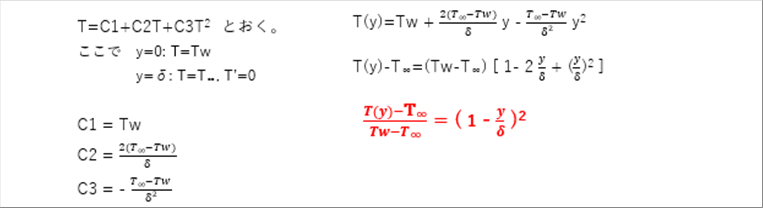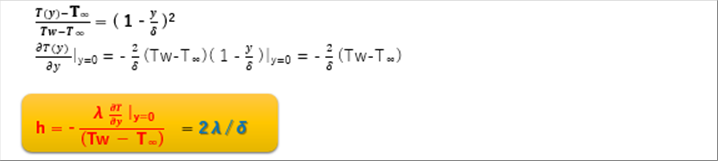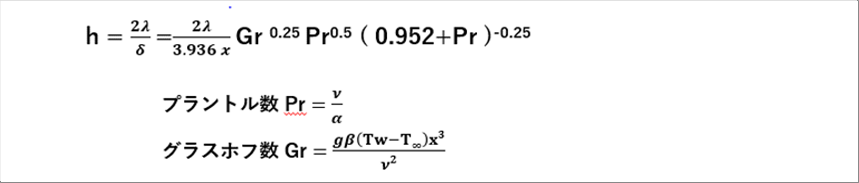対流熱伝達　Convectioin Heat Transfer
●　自然対流熱伝達係数の計算例　（丸鋼片）
●　自然対流と強制対流
●　自然対流の解析
●　熱伝達を知るにはどの範囲の流れを検討するのか
境界層内に適用する方程式の概要
熱伝達の式
●　非圧縮性流体のナビエストークスの方程式と連続の式
速度境界層
温度境界層
●　プラントル数と、速度・温度境界層の関係
●　速度分布
速度分布の想定
境界層内でのナビエストークスの方程式
速度分布の計算
●　熱エネルギーの式
温度分布の決定
●　熱伝達率の導出
境界層内でのナビエストークスの積分方程式
境界層厚さと速度の式
境界層内熱エネルギー積分方程式
境界層厚さ(速度は割愛）の決定
●　プラントル数Pr, グラスホフ数Gr、ヌセルト数Nu、境界層厚さδ
●　自然対流熱伝達率ｈ　位置による変化
●　強制対流熱伝達　ヌセルト数の実験式
丸鋼片、パイプに適したヌセルト数実験式
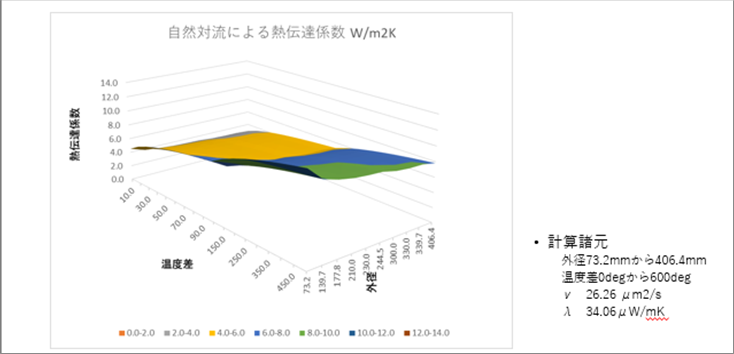
●　自然対流熱伝達係数の計算例　（丸鋼片）
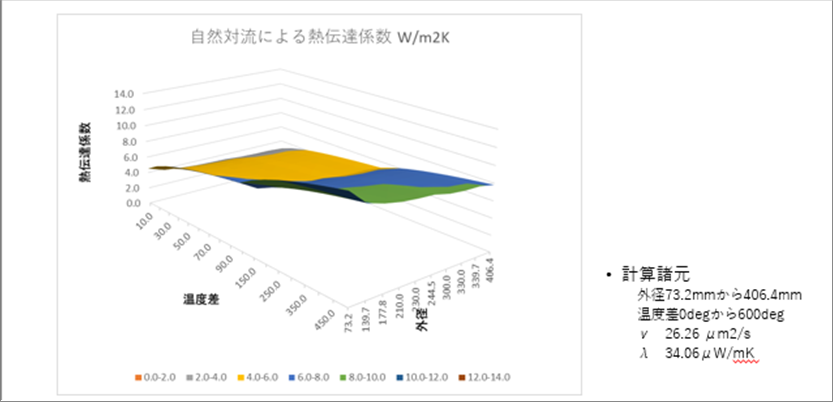
外径73mmから406.4mm, 温度差なしから600deg.までの熱伝達係数の計算結果です。おおむね6W/m2Kとなりました。
実際とあっているような気がします。シミュレーションでどう使うかはいろいろあると思いますが、基本的な考え方と計算方法をまとめました。
●　自然対流と強制対流
ものを置いてどのように冷えるかを考えてみたいと思います。
「物を置く」のは真空、気体、液体の中になります。このページは熱伝達の説明なので、気体か液体（流体）中に置くこととします。
冷たい例と熱い例を一つずつ上げれば、ドライアイスをシンクに置いたときに白い煙上がシンクの底に広がったり、キャンプファイヤーで火の粉が舞い上がっていく様子などです。この動きはそこにあるだけで自然に流れて行きます。
どうして動くかというと、周りの空気との温度差があるためです。温度差があると、熱は高温のものから低温のものに移動します。ドライアイスの場合は、高温の空気から低温のドライアイスに熱が移動し、キャンプファイアーでは、高温の炎から低温の空気に熱が移動します。熱い鉄の塊を空気中に置いた場合は、キャンプファイアーの場合と同様、高温の鉄から熱が空気に熱が伝わります。どの場合も、温度差が徐々に小さくなります。
風が吹いていない場合は、空気速度はゼロをみなせますが、この現象は発生します。これを自然対流による冷却（加熱）といいます。流体の速度を大きくするにしたがい熱移動は大きくなり、これは強制対流と呼ばれます。ただし、隕石が落下するように、速度が大きすぎると空気と物体の摩擦、ならびに、空気との断熱圧縮によって発熱し、両方の温度が上昇します。
被加熱材を加熱する炉床回転式加熱炉、ウォーキングビーム式熱処理炉などでは、燃焼ガスの流れがあるので強制対流といえますが、燃焼ガスと丸鋼片、パイプに温度差がある場合は自然対流も発生しているので、両方の検討が必要になります。被加熱材は通常炉の下面側におかれるため、ここでの燃焼ガス速度は平均速度より小さくなり、場合によっては強制対流が無視できるほど小さいこともあると思われます。したがって、ここでは、自然対流による熱伝達を考えたいと思います。
●　自然対流の解析
解析に使用する基礎式は、流体の運動方程式であるナビエストークスの方程式と、熱エネルギーの方程式ですが、どちらも2階微分方程式です。変数と同じ数の方程式が作れれば解が得られます。わかっている温度条件のほかにも、２階微分方程式を一回積分して得られる積分方程式も使えるので、変数と同じ数の方程式が作れる可能性は高いといえます。
前提条件として、気体は非圧縮性として扱うことにします。実際には、気体は圧縮性ですが、密度変化が５％までであれば、非圧縮性として扱って問題ないようです。マッハ数で0.3以下とのことなので、気体の速度が99.45m/s (358 km/h) 以下であれば非圧縮性として扱って差し支えないことになります。
●　熱伝達係数の実験式
自然対流の熱伝達係数はたくさんの実験式が報告されています。例えば、明治大学のHPの例では加熱か冷却か、上面にあるのか下面にあるのかなどで分類されています。
オペレーション的には、それらが利用できればいいのですが、実験式に使われているレイノズル数Re、プラントル数Pr、レイリー数Ra、ヌセルト数Nuなどの意味、例えば、ヌセルト数に熱伝導率（物性値。温度依存性あり。）をかけて距離で割ると熱伝達係数hになる理由を理解しておくのは有意義だと思われます。
●　熱伝達量を知るにはどの範囲の流れを検討するのか
伝熱量は、流れの速度、密度、熱伝達係数などに影響されますが、流体全体の解析は必ずしも必須ではなく、物体の周りの流れについてわかればよいと思われます。
物体の周りの流体の速度分布は、物体表面の速度＝ゼロで、物体から離れるにしたがって徐々に速くなり、十分離れると一定値になる。速度が変化する領域を速度境界層といいます。詳細は流体力学を参照してください。
同様に、流体の温度も変化しています。物体表面の流体温度＝物体温度で、物体から十分離れた場所で流体の温度になります。この領域を温度境界層とういう。速度境界層と温度境界層は必ずしも一致しません。
●　境界層内に適用する方程式の概要
ー　方程式
流体の運動方程式であるナビエストークスの方程式と、熱エネルギーの方程式は、これらの境界層内でも成り立つ。ただし、これらの方程式を解析的に解くことは非常にむつかしい（多分解けない）ので、工学的に問題ない範囲で条件を単純化する。
ー　自然対流の扱い
自然対流では、ナビエストークスの方程式の外力の項は浮力であり、この浮力で流体に速度が生じる。流体と物体が接する場所で高温部から低温部に熱エネルギーが移動する。この高温部から低温部へ移動する熱量が自然対流による熱伝達量である。
ー　空気の物性値の温度依存性　（「空気物性」参照）
加熱炉、熱処理炉では、流体が空気（燃焼ガス）の場合が多いが、空気の密度、粘度、熱伝達率などは温度に依存するので、適切な数値を使う必要がある。
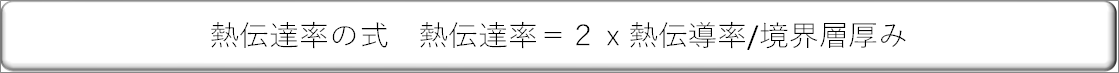●　熱伝達率の式　熱伝達率＝２ｘ熱伝導率/境界層厚み
物体表面の温度勾配がわかれば熱伝達率がわかる。物体表面の温度勾配を求めるため、ナビエストークスの方程式（流体の運動方程式）と、熱エネルギーの式を境界層内で解くことができれば解が得られる。結論は、熱伝達率＝２ｘ熱伝導率 / 境界層厚みとなる。
温度シミュレーション用に式だけが必要であれば、この結論だけで十分です。より深く理解するのも意味あることなので、その道筋を追ってみたいと思います。
●　非圧縮性流体のナビエストークスの方程式と連続の式
流体の運動に関係するのは、流体の密度、流入量、流出量、粘性、内部圧力、外力などで、それらを一度に表現したものがナビエストークスの方程式です。
ナビエストークスの方程式は、３次元流の運動方程式で、座標軸ごとに書いていくととてつもなく長くなります。プログラムを組むときには必要になりますが、読んでいくときには同じことを何度もみることになります。（きっとミスタイプも多くなると思います。。。。）
見たことのない人もいるかもしれませんが、こういう時はナブラ演算子、ラプラシアン演算子を使うと、見やすい式にまとめられます。これらの演算子を使えば、直交座標系、極座標系に関係なく同じ表現になります。
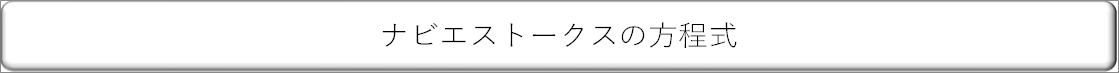ー　ナビエストークスの方程式
この式は、場所ｒと時間ｔで変化する流体の速度は、流体にかかる圧力ｐ、流体の粘性μ、外力ｆによってきまることを示しています。
ナブラ、ラプラシアンは、物理現象を数式であらわすときによく目にする演算子で、直交座標系での表記と比べると式の見やすさという点では利点があると思います。
ー　連続の式
流体の密度と速度が変化している場合の連続の式は次のようになります。
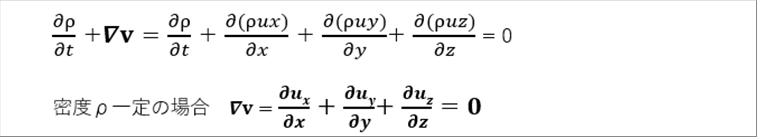流体が連続しているということは、流体が集まってくれば密度が上がり、逃げていけば密度が薄くなるということです。これなら、流体が切れて真空の場所ができたりしません。運動方程式は二階微分方程式なので複雑です、連続の式は１回微分だけなので、ナブラ演算子ではなく、直交座標系で書いても目が回りそうになることはありません。
●　速度境界層
物体の周りを流体が流れる時、流体の粘性よって物体の表面付近に速度が遅い領域「速度境界層」ができます。物体表面で速度ゼロ、99％の速度になるところが境界、物体から十分離れた場所では流れの速度になります。
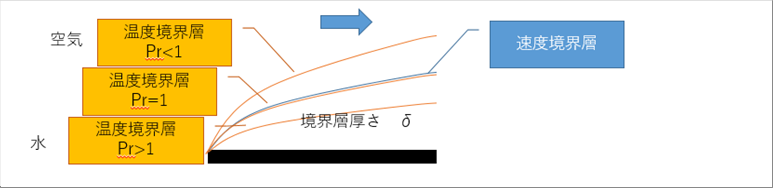
流れでは、常に層流か乱流かが問題になります。速度境界層でも層流と乱流で様相が異なります。ここでは自然対流の場合を考えているので、層流の場合を見ていけばいいと思われます。次の模式図は、前のものと同じですが、黒線の速度境界層一つに対し、赤線の温度境界層は３本書かれています。
●　温度境界層
温度境界層は、流体の速度が大きいと薄くなり、流体の粘度が高いと厚くなります。また、物体の表面での温度は、物体温度、物体から離れるにしたがって温度が変化し、物体から十分離れた位置で、流れの温度になります。物体のほうが温度が高い場合、低い場合があり、温度境界層内での温度分布は、速度境界層内の速度分布と必ずしも一致しません。
●　プラントル数と、速度・温度境界層の関係
プラントル数という無次元数が、速度境界層と温度境界層の厚みの関係の指標として使われています。ほかにもあるようですが、ここでは割愛します。
ー　プラントル数＝動粘度/熱拡散係数
Pr = ν(m2/s)/α(m2/s) = μ(Pa.s)Cp(J/kgK)/λ(W/kgK)
ν=μ/ρ、α=λ/ρCp
空気は温度によって密度、動粘度などが大きく変わるので、プラントル数がどう変化するかグラフにしみました。現場で空気を使う温度領域（３００K以上）では１より小さいので、空気の場合は、温度境界層は、速度境界層よりも薄いと思われます。
●　速度分布の想定
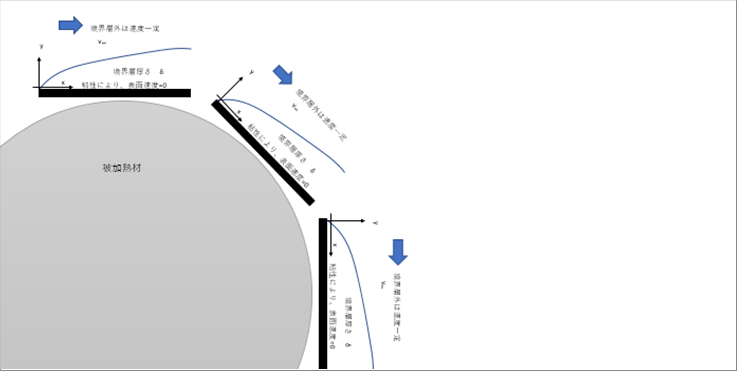
断面が丸い丸鋼片の場合を考察しておけば、四辺形断面の場合も使えると思われます。
上面、45°、側面の3つの場合を考えると、境界層厚みは違うが、同じような流れとなっていると推測できる。すなわち、境界層内では流体の速度は、粘性により表面での速度=０、境界層内で増速、減速して、v∞=0に戻る。
場所によって、支配的な速度成分が変わる。材料の上面では、ｖxが支配的で、側面ではｖyが支配的、45°は両方同程度と思われる。どの場合でも、表面から十分離れれば速度=ゼロになる。
したがって、速度は2回変曲点を持つので、位置の3次式が妥当と思われる。（境界条件は4つ必要。）
●　境界層内でのナビエストークスの方程式
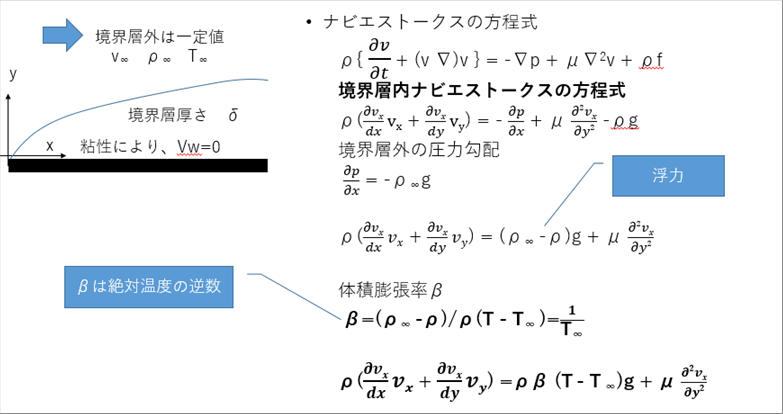
熱伝達率を計算するために必要な、境界層内のナビエストークスの方程式を導く。紙面に垂直方向ｚは被加熱材の長さ方向で、３元解析にはｚ軸も入れて計算すべきだが、計算を簡略化するために、ｚ軸方向への流れはないとする。
（　　）内は、微積分の式を展開する際によく使う手で計算を進める。（詳細は微積分基礎参照）
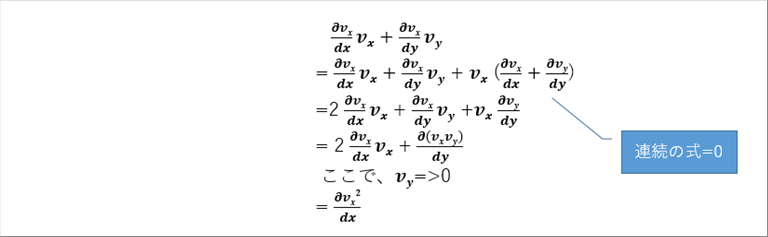（　　　）内は、x方向速度の２階微分となった。
境界層内のナビエストークスの方程式は、次式で与えられる。
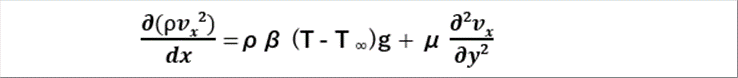●　速度分布の計算
境界層内の流体の運動方程式は求められたので、これを解き、境界層厚さδを計算していく。
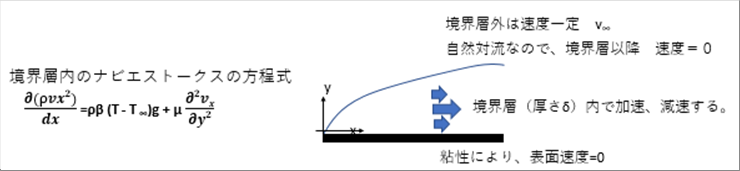境界層内の位置ｘでの速度vxは、y軸方向で変化する。計算を始める前に想定した通り、速度分布は変曲点が２回ある近似曲線で表現するのが妥当だと推測される。
VxとV∞の比で３次式を作ると、上の条件が同時に満足できるので、３次式の定数項を特定するように考えていく。
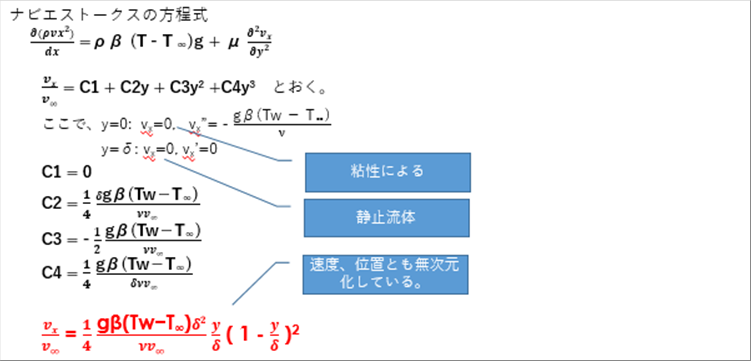「ここで」とある部分が境界条件で、式の上で説明した内容を使っている。
（１）粘性により、物体表面ｙ＝０で速度ゼロ Vx=0
（２）物体表面ｙ＝０の加速度変化率は（１）の条件を方程式に入れる。
（３）境界層上では、速度＝０。
（４）境界層上では、速度の変化＝０
未知数４，境界条件４なので３次式の定数項は確定できる。
●　境界層内のエネルギー方程式
●　境界層内温度分布の計算
物体表面では流体温度は物体表面温度で、そこから急激に温度が変化し、境界層から流体の温度となる。変曲点が１個なので、二次式で近侍できる。
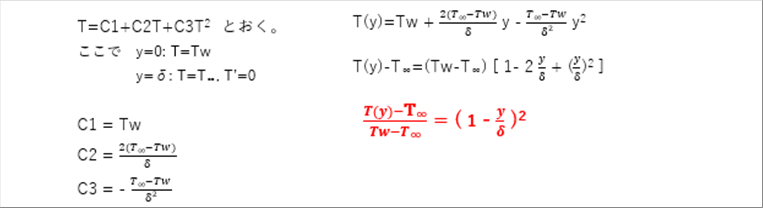●　熱伝達率の導出
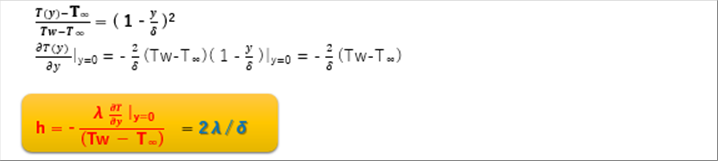物体表面y=0の温度勾配を熱伝達率の式に代入すれば、熱伝達率ｈは次の通りになる。
熱伝達率ｈ＝２ x 熱伝導率λ / 境界層厚みδ
境界層厚みδは、境界層内ナビエストークスの方程式から求められる。目次に書いた順に解いていくが、ここまで読み進めてきた根気強い方でも、まだ先が流そうだと思うとくじけそうになると思いますので、先に結論を書いておく。プラントル数、グラスホフ数、ヌセルト数のややこしい係数がどうして決まったが推測できると思います。
●　境界層内ナビエストークス積分方程式
●　境界層厚さと速度の式
●　境界層厚さと速度の未知数の決定
ー　境界層内熱エネルギー積分方程式
●　境界層厚さ(速度は割愛）の決定
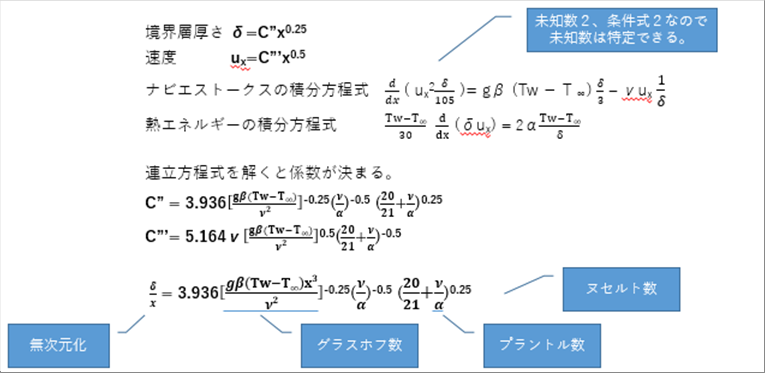
以上をまとめると次のようになります。
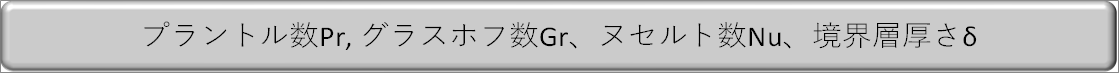●　プラントル数Pr, グラスホフ数Gr、ヌセルト数Nu、境界層厚さδ
プラントル数とグラスホフ数は次式で提案されている。これらは、各種の加熱、冷却条件での実験式を整理する際に使われます。
したがって、無次元化境界層厚さ δ/x は次式となります。
? δ / x = 3.936 Gr^( -0.25) x Pr ^ (-0.5) x ( 0.952 + Pr )^0.25
●　自然対流熱伝達率ｈ　位置による変化
前項でもとめた境界層厚さを熱伝達率の式に代入すると、熱伝達率ｈは以下のように求められます。
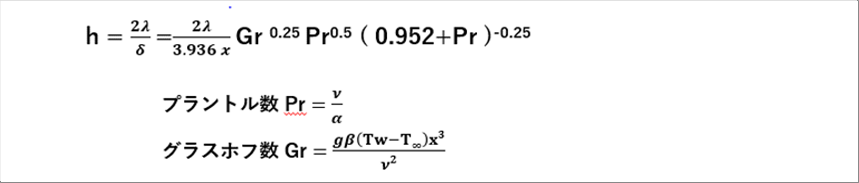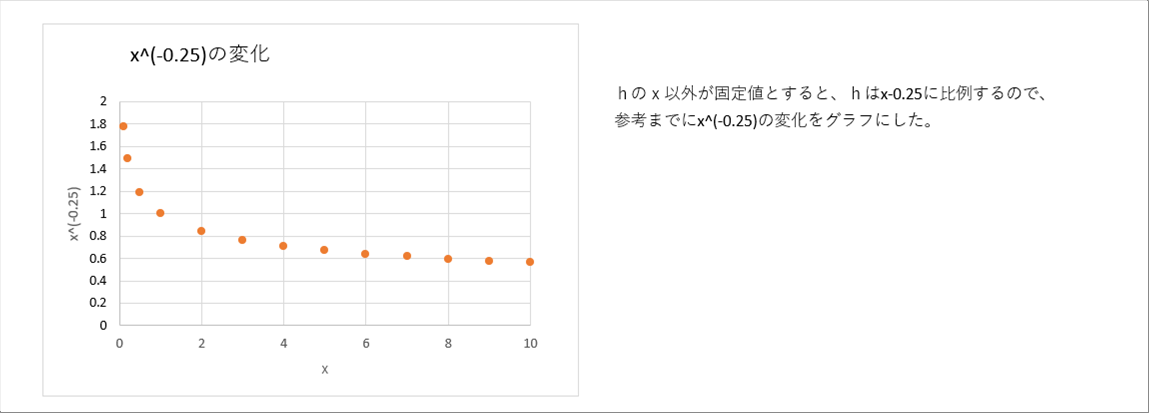
プラントル数、グラスホフ数とも温度、速度などに依存するのでｈがどのような変化をするのを想像するのは容易ではありません。ここでは、ｈの変化を想定するために、温度、速度などが一定の場合を考えます。この場合ｈは、ｘのの -0.25 乗に比例することがわかります。
このページの最初のグラフは、この式を使って自然対流熱伝達係数を計算したもので、温度と大きさで変化している。
●　強制対流熱伝達、ヌセルト数の実験式
前項は、「静止気体中」v∞=0として、自然対流の熱伝達係数を求めた。速度が小さい場合は自然対流の計算で問題ないと思いますが、ある程度速度が大きい場合は、強制対流を計算する必要があります。V∞を実際の速度として自然対流を計算したと同様に計算すれば、前項同様にラップトップなどで計算することもできると思います。
ヌセルト数がわかれば熱伝達係数が求まる。非常に便利なので、例えば、Nu = C (GrPr)m とおいて、係数Cと 係数mを実験的に決定する方法などが提案されています。計算機がなかった時代では、一択だった可能性もありますが、現在でも十分実用に耐えると思います。
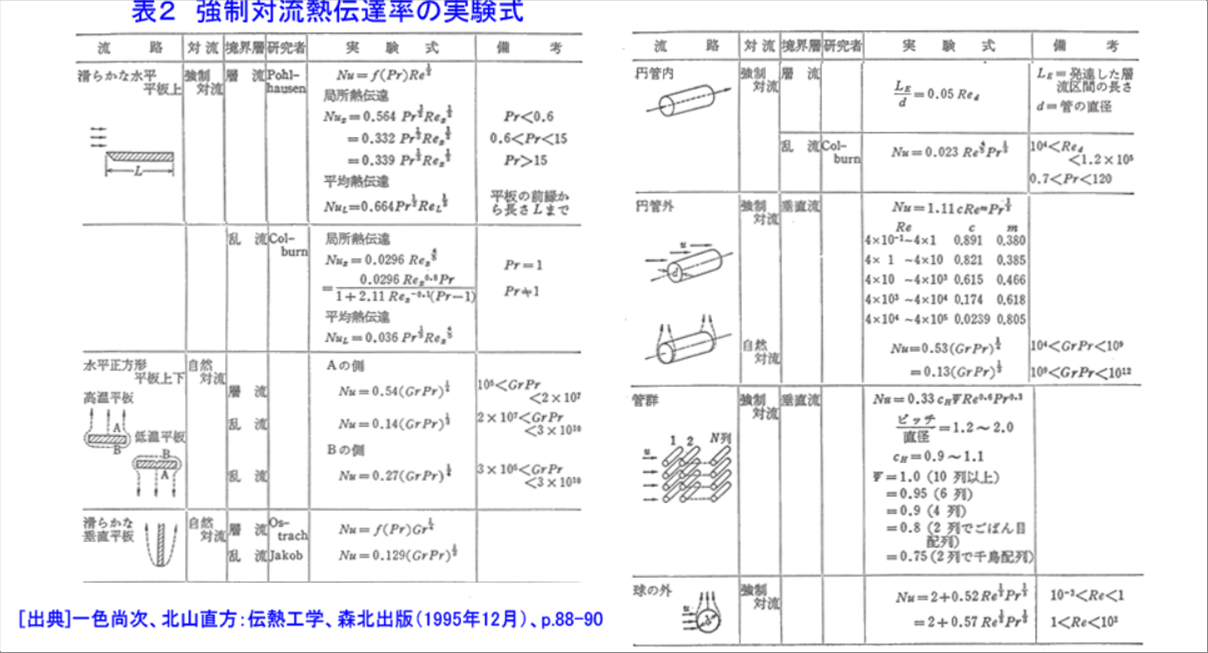
「原子力百科事典 ATOMICA」というウェブサイトでは、表２「強制対流熱伝達率の実験式」でいくつかの条件の実験式を紹介しています。当該ページには、出典として一色尚次、北山直方：伝熱工学、森北出版（１９９５年１２月）、ｐｐ８８−９０と記されています。
なお、レイリー数 Ra=GrPr を使った実験式もありますが、やっていることは同じだと思います。
いずれにせよ、我々の大先輩方は偉大ですね。
下の表は、Nu=C(GrPr)mと置いてCとｍを計算する方法の例です。
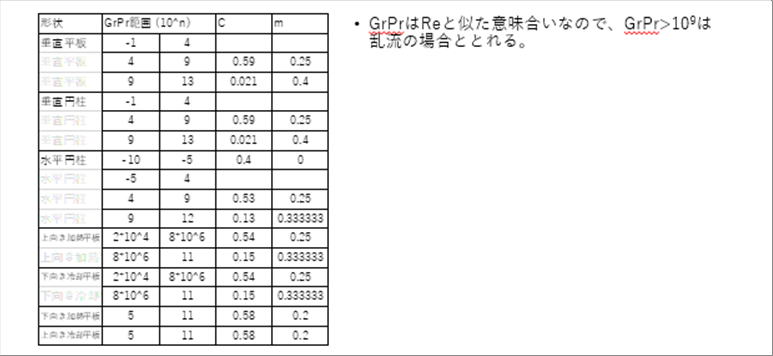次の表は、ATOMICAのサイトで紹介されている実験式の一例です。
Author: T. Oda
このページはエクセルで作り、excel2webでhtmlとcssを自動作成しました。