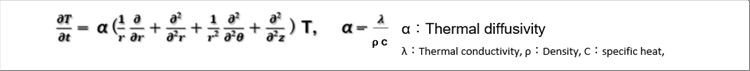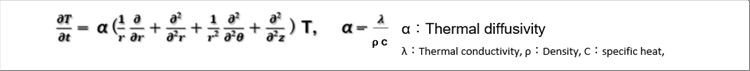| |
 |
| |
 |
| 1 Coordinate System Suitable for Temperature Simulation |
| 2 Microscopic Volume and Difference (Similar to Mesh) |
| 3 Fourie's Law |
| 4 Heat Conduction Equation |
| 4-(1) Cartesian Coordinate System |
| 4-(2) Cylindrical Coordinate System |
| 5 Solution of Heat Conduction Equation |
| 6 Heat Equilibrium in Macroscopic Volume |
| |
 |
| 1 Coordinate System Suitable for Temperature Simulation |
| |
| Heat Conduction Equations are used to calculate the temperature distributions inside an object in order to optimize the heat patterns for heating materials and heat treating products. |
| |
| For round steel bars and pipes, cylindrical coordinate system (r, angle, z) is convenient, and for square cross section bars and plates, Cartesian one (x, y, z) is convenient. |
| |
| The reason is because since the shapes and coordinate systems match, it is easy to generate the mesh and input boundary conditions. Advantages include fewer input errors and faster verification. |
| |
 |
| 2 Microscopic Volume and Difference (Similar to Mesh) |
| |
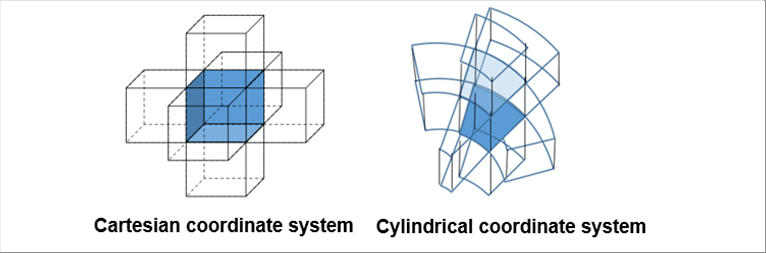
| The following pictures show the microscopic volume surrounded by six (6) neibor volumes. |
| |
 |
| |
| Dividing a continuous range is called difference. The microscopic volume can be equal to each axis. |
| |
| The difference in cylindrical coordinate is large in the cells at the outer periphery and becomes smaller and smaller toward the center. Please note that the center becomes a singular point. It has been proposed to treat the small area around the singular point as an ellipse. However, we may omit the ellipse if we start the calculation from the minimum radius, say 0.001, so that the effect on the whole can be ignored. It will not seem to be an error of big impact. |
| |
 |
| 3 Fourie's Law |
| |
| The Fourie's law is given as follows. |
| |
| The amount of heat transferred is proportional to the temperature difference (temperature gradient) and flow from a high temperature place to a low temperature place, Therefore, the sign is negative. |
| |
 |
| |
 |
| 4 Heat Conduction Equation |
| |
| Heat is energy, and the law of conservation of energy holds true for the heat. The heat counduction equation is derived from the law. |
| |
| Regardless of whether heat is generated just due to the flow of thermal energy, the law of conservation of thermal energy as a formula is that "incoming heat + heat generation = increase/decrease in thermal energy + outgoing heat." For the temperature simulation we want to know the temperature. so, let's convert the "increase/decrease heat" in the equation to "increase/decrease temperature" using the Fourie's law of cooling. the increase/decrease heat is first derivative of heat, therefore, the increase/decrease temperature becomes the equation for the second-order of temperature. By modifying the equation , the final heat conduction equation is as following. |
| |
 |
| |
| Here, the thermal diffusivity is thermal conductivity divided by density and by specific heat. |
| |
| The equation expressed in Laplacian is common to all coordinate systems |
| |
 |
| 4-(1) Cartesian Coordinate System |
| |
| The heat conduction equation in the Cartesian coordinate system is as follows. |
| |
 |
| |
| If there is no heat generation, the last terms is omitted. |
| |
 |
| |
| The differential equation can be solved using the variable separation method. See "Analytical Solution" for detail. |
| |
 |
| 4-(2) Cylindrical Coordinate System |
| |
| If there is no heat generation, the heat conduction equation in cylindrical coordinate system is as follows. |
| |
| |
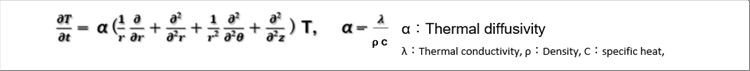 |
| |
 |
| 5 Solution of Heat Conduction Equation |
| |
| Analytical solution to heat conduction equation cannot be solved except in exceptionally special case. |
| For information on how to obtain the analytical solutions using the variable separation method, see "Analytical Solution." |
| |
| Due to this reason, methods have been proposed in which, based on the temperature distribution at a certain time, the temperature distribution after a small period of time is sequentially calculated numerically. See "Numerical Analysis" for detail. |
| |
 |
| 6 Heat Equilibrium in Macroscopic Volume |
| |
| For detail informationi about Cartesian coordinate system, please see "Analytical Solution." |
| |
 |
| |
| For detail information about cylindrical coordinate system, please see "Fourie's law (r, angle, z)." |
| |
 |
| |
| |
| |
| |
| |
| Author: T. Oda |
| The page was prepared in Excel, and html and css files were automatically generated by the excel2web. |