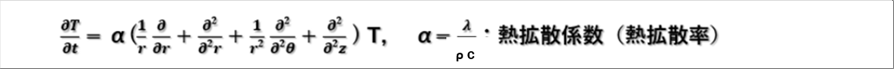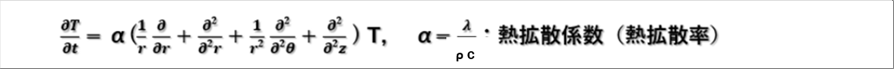| |
 |
| |
 |
| ● 温度シミュレーションに適切な座標系は |
| ● 微小領域、差分 (メッシュ切りとほぼ同じ。) |
| ● フーリエの法則 |
| ● 熱伝導方程式 |
| 直交座標系 |
| 円柱座標系 |
| ● 熱伝導方程式の解 |
| ● 微小領域の熱のつり合い |
| |
 |
| ● 温度シミュレーションに適切な座標系は |
| |
| 材料の加熱、製品の熱処理のヒートパターンを最適化するために、物体内部の温度分布を計算する必要があるが、この時の計算に伝導方程式が使われる。 |
| |
| 丸鋼片、パイプでは、円柱座標(r、θ、z)が便利で、四角断面のものは直交座標系(x、y、z)が便利である。 |
| |
| 理由は、形状と座標系がマッチしているので、メッシュの切り方、境界条件の入力が簡単にできる。このため、入力間違いが少なく、かつ、確認も短時間で済ませられる利点がある。 |
| |
 |
| ● 微小領域、差分 (メッシュ切りとほぼ同じ。) |
| |
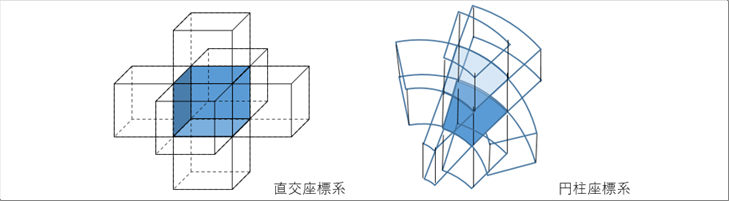
| 微小領域と、その周囲の微小領域は下のようになっている。 |
 |
| |
| 連続している領域を分割することを差分というが、微小領域は、各軸に対して均等にすることができる。 |
| |
| 円柱座標の差分は、外周部のセルが大きく、中心にいくにしたがって小さくなる。また、円柱座標では中心部は特異点となる。特異点の扱い方法は円に極めて近い楕円にするなどが提案されているが、温度シミュレーションをする場合は、半径の最小値を0.001にするなど、全体への影響を無視できるくらい小さくすれば大きな誤差にはならないと思われる。 |
| |
 |
| ● フーリエの法則 |
| |
| フーリエの法則は次式で与えられる。 |
| |
| 移動する熱量は、温度差(温度勾配)に比例し、温度が高いところから低いところへ流れるので、符号はマイナスとなる。 |
| |
 |
| |
 |
| ● 熱伝導方程式 |
| |
| 熱はエネルギーであり、エネルギー保存の法則が成り立つ。この法則から熱伝導方程式が導かれる。 |
| |
| 熱エネルギーが流れるだけで発熱するかどうかはさておき、「微小領域の熱エネルギーが保存されている」ことを式で書くと、「入熱+発熱=内部エネルギー増減+出ていく熱」となる。温度が知りたいので、式中の「熱の変化」をフーリエの法則で「温度の変化」に変換すると、熱の変化(1階微分)は、温度の2階微分の式になる。式を変形させていくと、最終的に熱伝導方程式は次式で与えられる。 |
| |
 |
| |
| ここで、αは熱拡散係数(もしくは熱拡散率)といい、熱伝導率λを密度ρと比熱Cで除したものです。 |
| |
| 一般式は、直交座標系、円柱座標系ともに同じ表現になります。 |
| |
 |
| ● 直交座標系 |
| |
| 一般式の直交座標系は次式で与えられる。 |
| |
 |
| |
| 発熱がない場合は、次式となる。 |
| |
 |
| |
| この微分方程式は、変数分離法で解くことができる。詳細は「解析解」を参照してください。 |
| |
 |
| ● 円柱座標系 |
| |
| 発熱がない場合、一般式の円柱座標系は次式で与えられる。 |
| |
| |
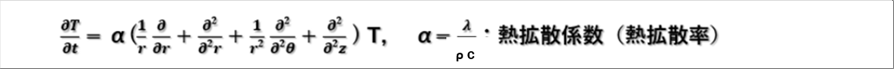 |
| |
 |
| ● 熱伝導方程式の解 |
| |
| 熱伝導方程式は、例外的に特別な場合を除き解析的な解は得られない。 |
| 変数分離法による解析解の求め方は、「変数分離解」参照。 |
| |
| このため、ある時刻の温度分布をもとに、微小時間経過した後の温度分布を逐次数値計算する方法などが提案されている。(数値計算を参照してください。) |
| |
 |
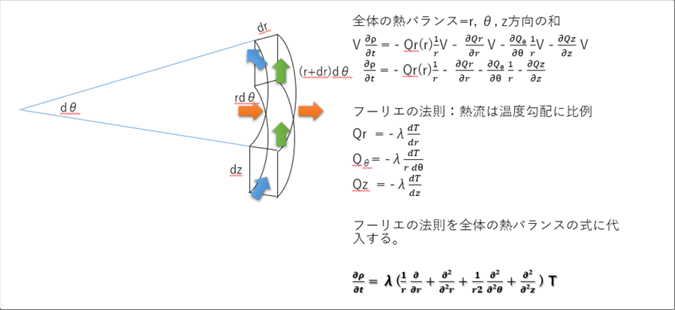
| ● 微小領域の熱のつり合い |
| |
| 直交座標系の詳細は、「変数分離法」を参照してください。 |
| |
 |
| |
| 円柱座標系は、「熱伝導(r,θ,z))」参照してください。 |
| |
 |
| |
| |
| |
| |
| |
| Author: T. Oda |
| このページはエクセルで作り、excel2webでhtmlとcssを自動作成しました。 |