最小着火エネルギー、着火時間、熱損失 MIE, Ignition Time, Heat Loss
1 失火か点火の分岐点
2 参考文献
3　定義
3-(1) 臨界熱流束Critical Heat Flux CHF
3-(2) 最小着火エネルギー Minimum Ignition Energy J
3-(3) 着火時間 Ignition Time
3-(4) 燃焼速度 Burning Velocity
3-(5) 消炎距離 Quenching Distance
4 最小着火エネルギーと消炎距離 Minimum Ignition Energy and Quenching Distance
4-(1) 気体燃料の最小着火エネルギー
4-(2) 消炎距離と最小着火エネルギー Quenching Distance and MIE
5 着火に要する時間 Time to Ignite
5-(1) 熱流束 Heat Flux
5-(2) 火炎温度と発火温度 Flame Temperature and Ignition Temperature
5-(3) 電気スパークのエネルギー Electric Energy of Spark
5-(3)-1 コイルのエネルギー Electric Energy of Coil
5-(3)-2 コンデンサーのエネルギー Electric Energy of Condenser
5-(4) やすり式ライターの火花温度 Flint Lighter Spark Temperature
5-(5) 熱損失の原因と対策 Reasons and Countermeasures for Heat Loss
5-(5)-1 熱損失の原因 Causes of Heat Loss
5-(5)-2 熱損失の対策 Countermeasures for Heat Loss
5-(5)-3 熱損失の想定 Assumtion of Heat Loss
5-(5)-3-a 火球の熱損失 Heat Loss of Fireball
5-(5)-3-b 電光の熱損失 Heat Loss of Lightening
5-(5)-3-c 失火の可能性 Possibility of Misfire
1 失火か点火の分岐点
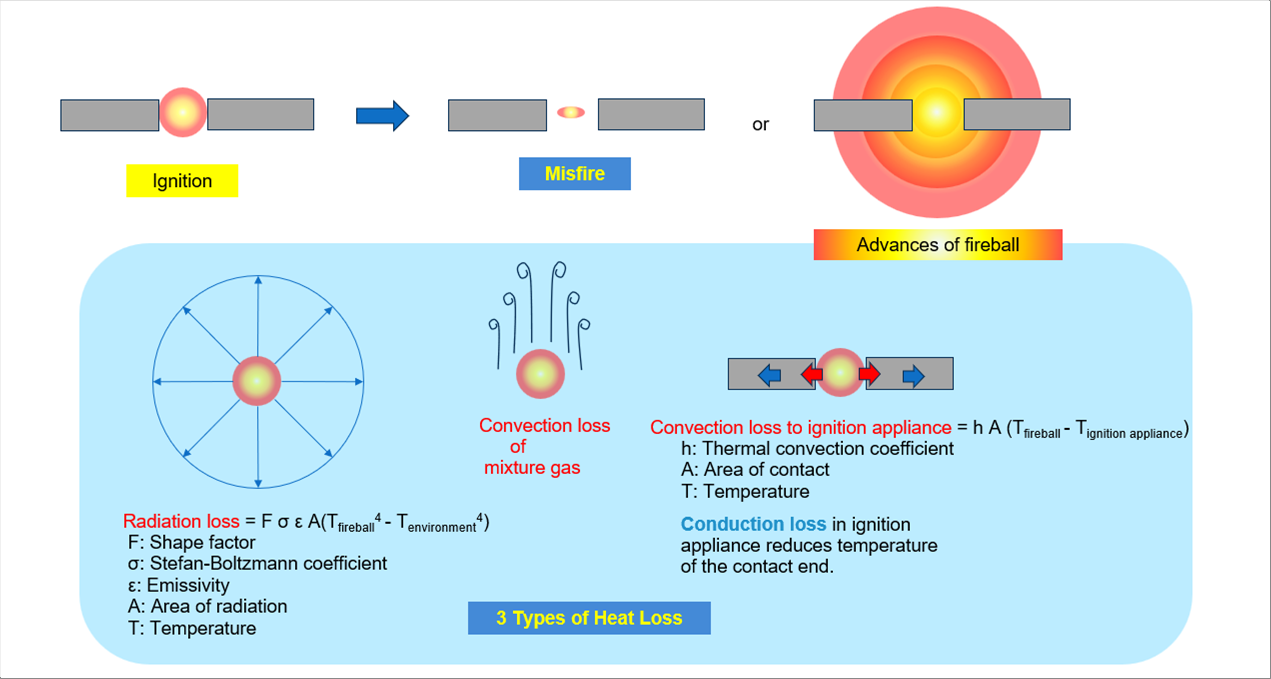
下の絵は、何らかの点火器具を使って点火する場合、失火して点火に失敗する場合と、火球が進展して点火に成功する場合を模式的に描いたものです。失火するか火炎が進展するかは、その下に書いた３種類の損失の程度によります。
熱力学的に言えば、熱流束が限界熱流束より大きく、損失を除いた熱が最小着火エネルギーより大きければ着火に成功し、燃焼が継続します。損失は、熱輻射 radiation、熱伝達 convection、熱伝導 cunduction の３つが原因で発生し、発火器具自体、燃料混合気、チャンバー壁などに伝わって失われ、避けることはできません。
熱輻射、熱伝達、熱伝導による損失の計算式をイラストの下に書いてあります。詳しくは、熱力学のそれぞれの項目で説明していますので、そちらを参照してください。。
このホームページでは、着火するための条件である、最小着火エネルギー、消炎距離、着火方法、熱損失、着火にかかる時間を考えていきたいと思います。
2 参考文献
最小発火エネルギーと消炎距離のデータは、安全工学 pp.296-pp.309, Vol.7 No.4 (1968),　秋田先生（東京大学工学部）がまとめられたデータを使わせていただきました。
５ページ以上にわたって各種材料の燃料濃度、酸素濃度、圧力で最小発火エネルギーと消炎距離を記載されています。
燃焼速度は、Gregory T. Linteris と John L. Pagliaro 著 Burning Velocity Measurements and Simulations for Understanding the Performance of Fire Suppressants in Aircraft, NIST Technical Note 1904　によりました。
着火までかかる時間については、James G. Quintiere 著 Principles of Fire Behavior SECOND EDITION の式を使わせていただきました。
電気式点火器具の一例としてエンジン用のプラグを使わせていただきました。NGK 日本特殊陶業株式会社　自動車関連製品　お問い合わせ窓口に、プラグの電極の消炎距離の考え方、プラグの静電容量についてお聞きして回答をいただきました。
このホームページの内容に間違いがある場合は、筆者の解釈の間違いで、参照元の責任ではないことをお断りしておきます。
3　定義
3-(1) 臨界熱流束Critical Heat Flux CHF
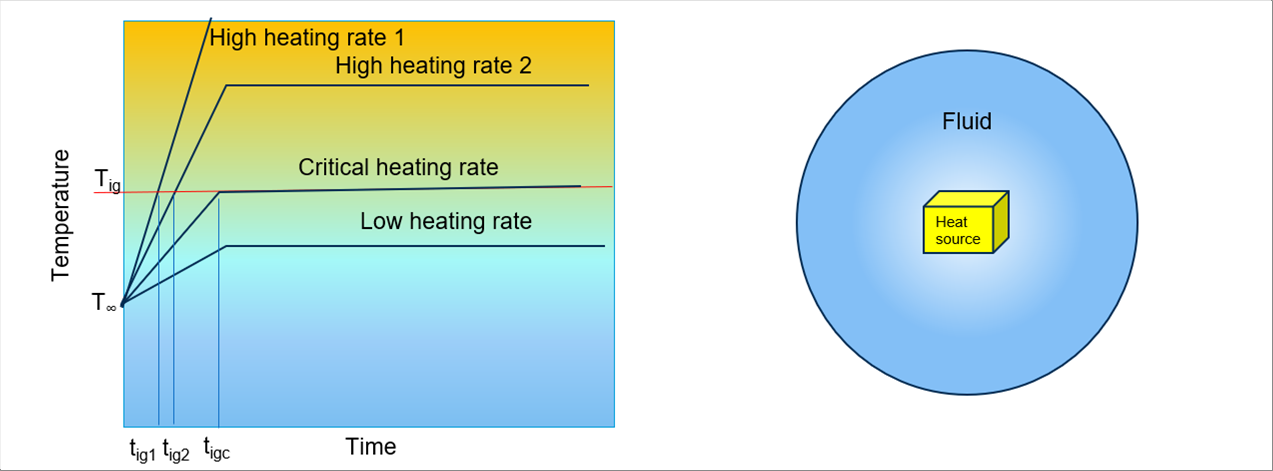
ある熱量を持った熱源を流体に入れると、温度の高い熱源の表面から、温度の低い流体に熱が移動します。単位時間に単位面積当たりの熱量の移動を熱流束といい、W/m2で表されます。
熱流束により、流体の温度が上昇します。
流体が液体の場合、十分な熱流束があれば液体はやがて沸騰しますが、あるレベル以下の熱流束では沸騰しません。
流体が可燃性気体の場合と酸素や空気の爆発範囲の混合気の場合、十分な熱流束があればやがて燃焼が始まります。あるレベル以下の熱流束では、燃焼が始まりません。
このように、液体が沸騰する限界の熱流束、爆発範囲の気体が燃焼する限界の熱流束を臨界熱流束と言います。
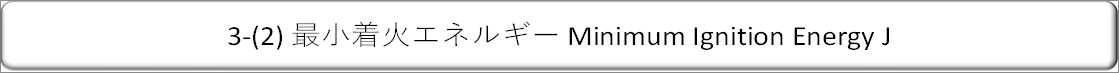3-(2) 最小着火エネルギー Minimum Ignition Energy J
水素、メタン、プロパンなどの気体燃料と空気の混合気に電極を入れてスパークで発火させる場合に、どういう条件で混合気に着火するかを考えてみます。
スパークによって発生した熱は、混合気を加熱するだけでなく、混合気の対流を発生し、電極への熱伝達などにも消費されます。混合気の温度が発火点に達すると着火します。これを最小発火エネルギーと言います。下の絵は、混合気に差し込んだ電極付近を表しています。
熱損失は、輻射、伝達、伝熱によって発生します。まず、輻射は、スパークの電磁波（可視光を含みます。）エネルギーがあらゆる方向に向けて伝わります。次に、スパークによる周囲の混合気の温度上昇による自然対流が発生し、その一部が電極表面に達して熱伝達が起こります。電極に伝達された熱は、システム全体に伝導します。
スパークの総エネルギーが、損失より大きいとスパーク付近の混合気温度が上昇し、一定の時間経過の後に混合気温度が発火点に達すると発火します。
3-(3) 着火時間 Ignition Time
着火時間とは、混合気が爆発範囲にあり、着火元から臨界熱流束以上の熱流束がある場合に、着火にかかるまでの時間をいいます。最小着火エネルギーを熱流束で除した数値です。
3-(4) 燃焼速度 Burning Velocity
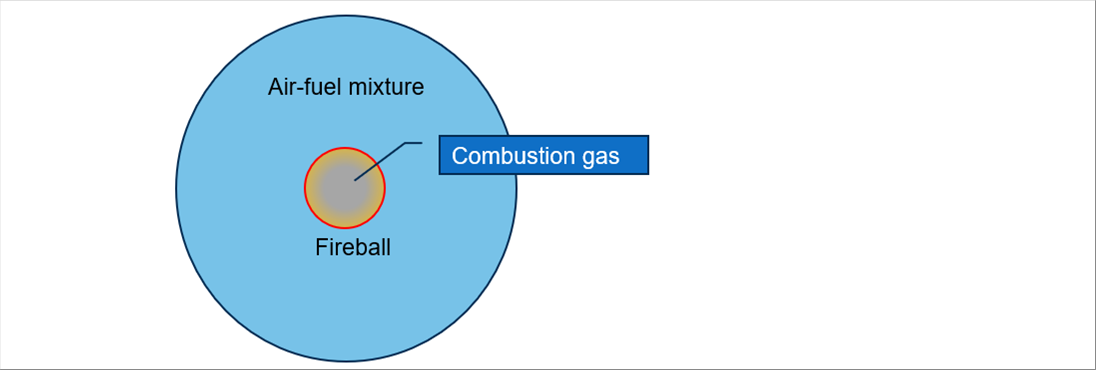
熱源を球と考えます。着火すると火炎面ができ、それが広がります。火炎面は、燃焼後の領域と燃焼前の領域の境界になります。
火炎面は、厚みゼロで均一とします。火炎面の進展により圧力が発生します。燃焼後の成分は平衡状態にあり、燃焼前後とも理想気体で、熱容量は温度依存性があり、断熱とします。燃焼前の混合気は、火炎面で等エントロピー圧縮されるとします。
この条件で、燃焼速度は次式で与えられます。
3-(5) 消炎距離 Quenching Distance
着火している電極を次第に近づけていくと、ある距離までは着火エネルギーは変わりませんが、ある距離になると急激に必要エネルギーが増加し、限界点を超えるとどんなにエネルギーを加えても着火しなくなる。この距離を消炎距離といいます。
着火しない理由は、損失が大きくなり、スパークのエネルギーが混合気の温度上昇に有効に使われなくなるからです。電極間距離を小さくすると、電極への熱伝達が大きくなり、加熱システム内への熱伝導で熱が逃げるためと思われます。
即ち、着火元は燃焼が始まるまでの時間、燃料の着火点以上の温度を保持する必要があります。
4 最小着火エネルギーと消炎距離 Minimum Ignition Energy and Quenching Distance
4-(1) 気体燃料の最小着火エネルギー
安全工学の資料には可燃性液体と可燃性気体の最小着火エネルギーが数多く示されています。パラメーターは、燃料割合、大気中の酸素比率、圧力で、ここでは、気体燃料の成分である水素H2、メタンCH4、エタンC2H6、エチレンC2H4、プロパンC3H8の最小着火エネルギーを紹介します。
下の表は、エタンの例です。
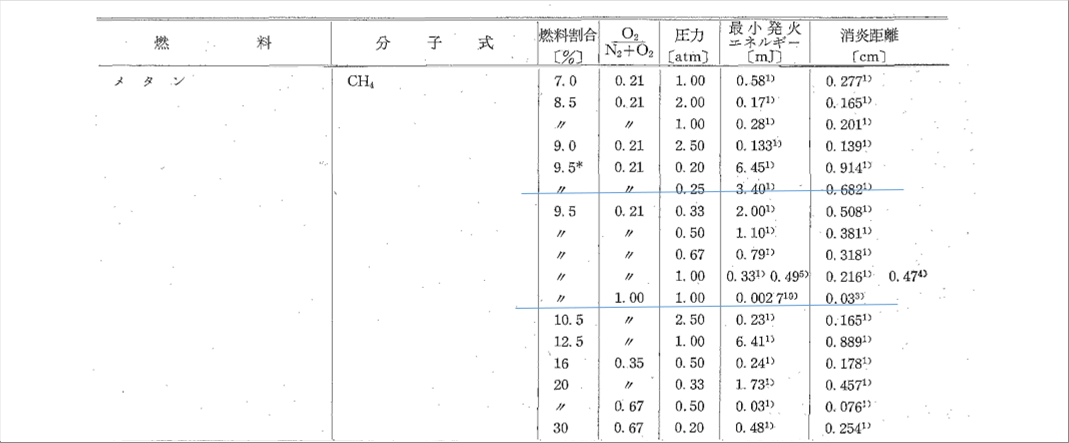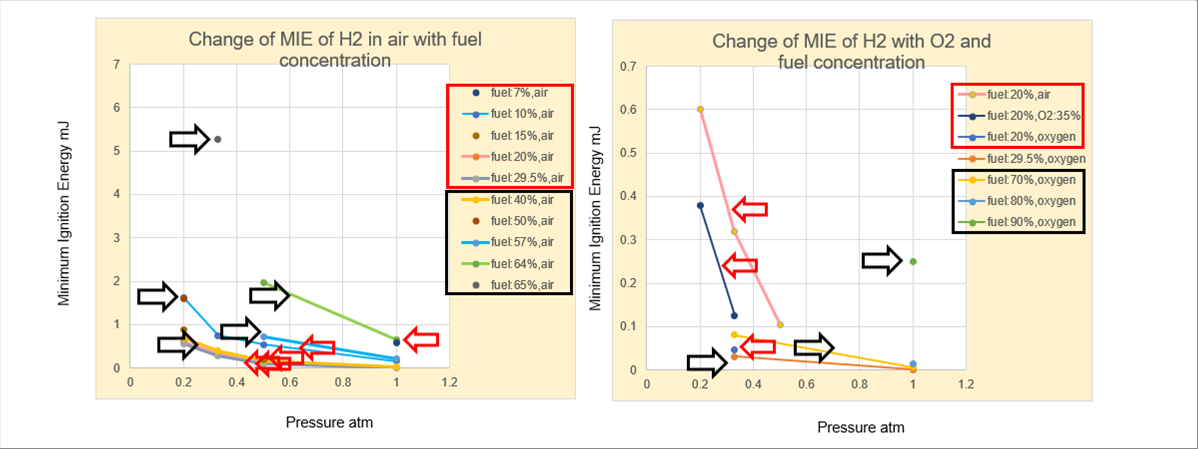
下のグラフは、データ数が最も多かった水素の最小着火エネルギー（MIE）です。左図は、空気中で燃料濃度が変化した場合です。右図は、燃料濃度20%で、酸素濃度が21%, 35%、100%になった場合です。酸素濃度100%で、燃料濃度を20%から90%まで変化した場合です。
赤枠で囲った部分は、MIEが小さくなり、黒枠では大きくなることを示しています。空気中（左図）でも、酸素中（右図）でも、燃料がある割合まではMIEは小さくなりますが、そこを超えると大きくなります。どちらも、水素濃度30%ほどで最小です。
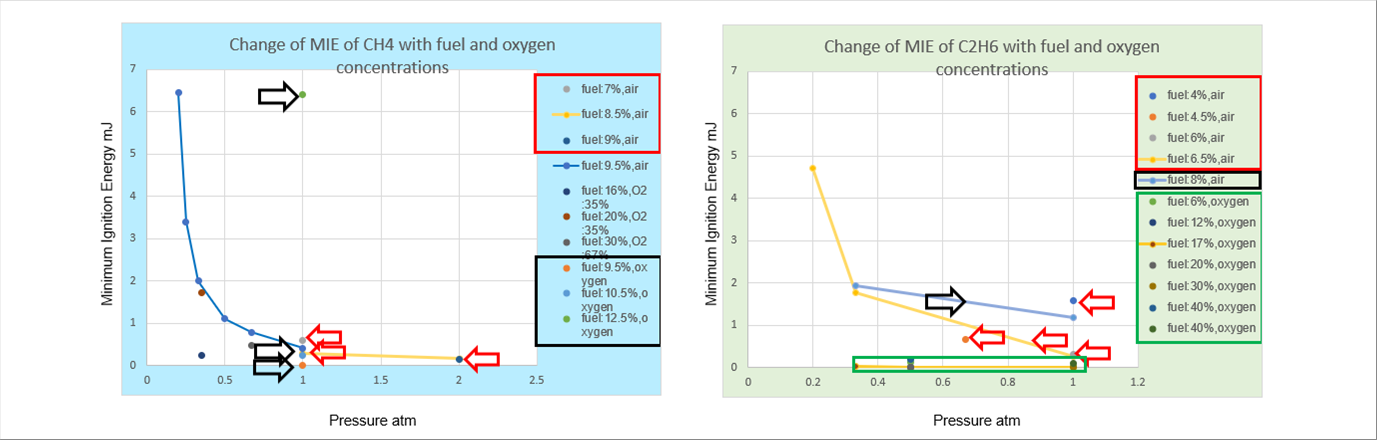
下のグラフは、メタンCH4とエタンC2H6のMIEです。
メタン濃度と酸素濃度がMIEに及ぼす影響は水素の場合と同じです。メタンは濃度9%程度で最小のMIEになり、9.5%では若干増加します。メタン濃度9.5%で、酸素中ではMIEは急激に小さくなりますが、12.5%では数十倍に急増しています。水素のMIEは空気中で濃度30％程度まで下がり続けますが、メタンでは空気中で9.5%、酸素中でも12.5%で大きな値を示すので、着火しにくいと言えると思います。
エタンの空気中MIEはエタン濃度%6.5%程度まで小さくなりますが、8.5%では増加に転じています。酸素中では、MIEは急激に減少します。酸素中では、濃度30%で増加に転ずるようですが、小さな値をキープしています。
4-(2) 消炎距離と最小着火エネルギー Quenching Distance and MIE
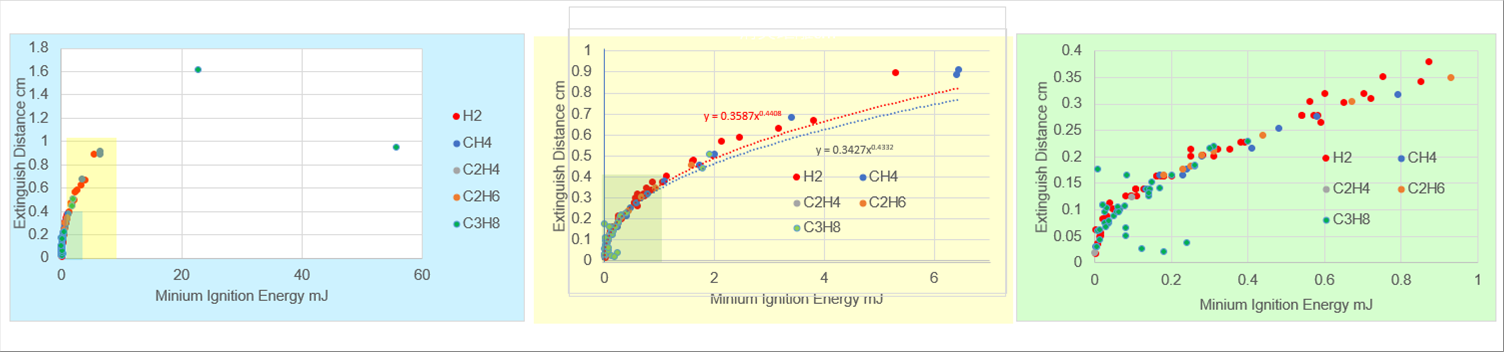
下の３個のチャートは、水素、メタン、エタン、エチレン、プロパンの消炎距離と最小着火エネルギー（MIE）の相関図です。酸素濃度は21%から100%、燃料濃度は4%から90%、圧力は0.089atm(9kPa)から5.2atm(527kPa)と広範囲にわたっていますが、ほぼ同じ傾向を示しています。
中央のグラフは、全体図のイエローの範囲です。右のグラフは、グリーンの範囲です。
参考までに、中央のグラフに回帰式を追加しました。回帰式は２本ありますが、どちらが正解というものではありません。必要な範囲と燃料を決めて回帰式を作れば、精度いい回帰式が得られると推測されます。
5 着火に要する時間 Time to Ignite
定義に描いたように、電極間に発生するスパークは、電極間距離を直径とする厚さゼロの球体の表面としました。火炎の内部は燃焼済み、外部は未燃焼と想定しました。火炎の内部が着火するので、電極間距離は少なくとも消炎距離より大きいとします。
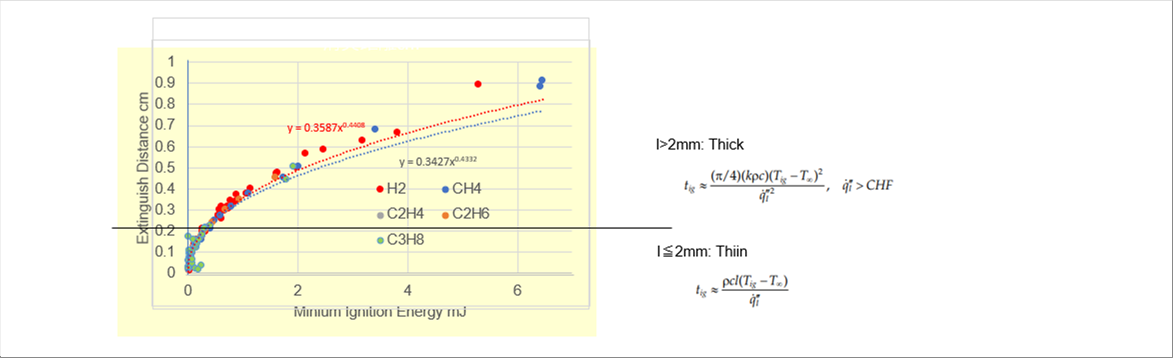
前項の消炎距離は、0.19mmから16.2mmです。2mm以下を「薄い」、それより厚い場合「厚い」とします。消炎距離は最小着火エネルギーとよい相関を示すと想定されるので、最小エネルギーで決めてもいいと思います。
薄い物体の発火に要する時間と厚い物体の発火に要する時間 tig は、次式で与えれれます。絵のサフィックスLは、熱損失を表していますが、燃焼の初期にはゼロと想定しています。熱損失は加熱されると大きくなり、十分時間がたつと、熱流速と同じになり、温度差がなくなります。詳細の導出方法は「１はじめに」に記載の資料を参照ください。
これは固体の式ですが、混合気体の着火元の周囲を加熱する場合にも適用できると思うので、この式のパラメーターが混合気で何を指すかを見ていきたいと思います。初期温度、着火温度は一定値です。密度、比熱は温度依存性がありますが、連続的に変化するので関数として表現できます。（通常は回帰式を作ります。このホームページでも空気の場合の３次式を挙げています。）熱流束は、熱伝導率と温度差の積を距離で除算して求められます。
5-(1) 熱流束 Heat Flux
熱流束は、単位面積当たりの熱の流れ量で、次式で与えられます。（詳細は熱力学を参照してください。）
低温部の温度は室温なので、高温部の温度がわかれば計算できます。高温ぐは、着火元の温度です。混合気の着火は通常パイロットバーナーによるものが多いと思われます。
5-(2) 火炎温度と発火温度 Flame Temperature and Ignition Temperature
混合気は、爆鳴気の状態だと仮定します。混合気全体が完全燃焼して、水蒸気と二酸化炭素になる際に発熱します。これが高位発熱量です。酸素の場合は、水蒸気と二酸化炭素を加熱し、空気の場合は、さらに窒素を加熱します。このため、空気の場合の火炎温度は酸素の場合より低くなります。
高温時には、生成物が乖離して平衡状態になります。乖離は吸熱反応なので、この分を差し引いた熱量で燃焼ガスの温度が上がります。燃焼後のガスは、温度が上がる際に仕事をしない前提で考えると、定圧比熱を使うことができます。
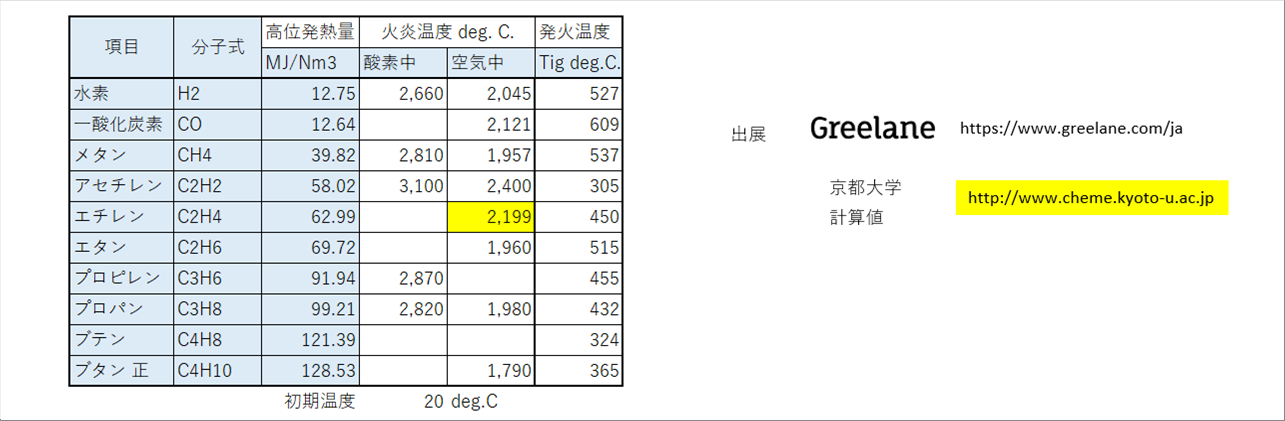
次の表は、代表的な気体燃料の高位発熱量、火炎温度、自然発火温度です。パイロットバーナーの空燃比が１の場合は、空気中の列の温度が火炎温度になります。パイロットバーナーに着火するためには、自然発火温度以上に加熱する必要があります。
上の表のエチレンの値は京都大学の計算値ですが、計算の説明文を式にすると、次のようになります。
気体の比熱は、温度依存性があります。「数値解析」の「空気物性」で、空気の比熱をグラフにプロットして、変曲点が２か所あったので温度の３次式に回帰しました。同様の回帰式を二酸化炭素、水蒸気、窒素について作れば積分可能です。積分すると温度の４次式になるので、できた４次式を解けば火炎温度Tが得られます。
ただし、下の化学式のように、高温では気体が乖離しています。乖離は吸熱反応なので、その分の熱量Q1, Q2, Q3を、高位発熱量Qから減算する必要があります。
5-(3) 電気スパークのエネルギー Electric Energy of Spark
混合気に着火する方法の一つとして、電気スパークがあります。どのくらいのエネルギーになるのか検討してみたいと思います。一般的な交流電源のスパーク発生回路を下に示します。
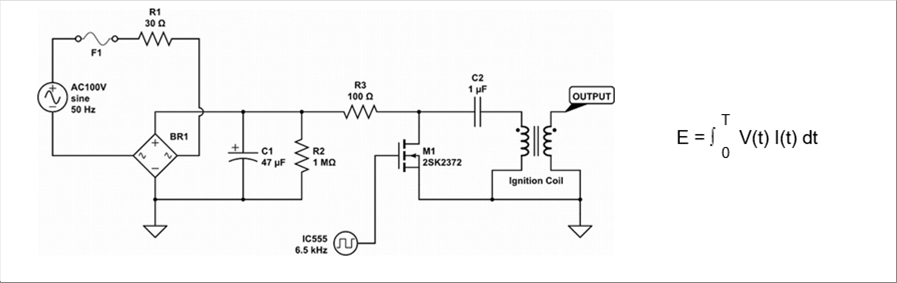コイルのインダクタンスがありませんが、ブリッジで全波整流した脈流を、タイマーとスイッチでコイルに6.5kHzの交流を供給しているようなので、LC回路の共振周波数の公式より、インダクタンスは600μHだと思います。
電極間に発生するスパークのエネルギーは、上図のoutputから得られます。エネルギーは、電圧と電流の積で表されます。スパーク発生時の電圧と電流は、徐々に小さくなりゼロになります。したがって、スパークが持続している時間の総エネルギーは、電圧と電流の積の積分値になります。
なお、車やバイクのスパークプラグ用の高電圧発生回路は、バッテリーの直流１２Vを交流に変換してイグニッションコイルで高電圧を発生させ、スパークプラグに供給しています。スパークプラグはコンデンサーとして使われています。コンデンサーが発生するエネルギーは、静電容量と電圧の２乗の積に比例するので、バッテリーの電圧をコイルで３万ボルトに昇圧すると、プラグでは数百万倍のエネルギーが得られます。
上の回路の出力エネルギーは、実際の出力波形で数値積分する必要があると思いますが、スパークの実際の出力波形の計測も困難だと思われ、２次側の配線で計測する場合が多いようです。このホームページでは、計算が簡単なコイルとコンデンサーそれぞれ単独の直流回路で、エネルギーを計算してみたいと思います。
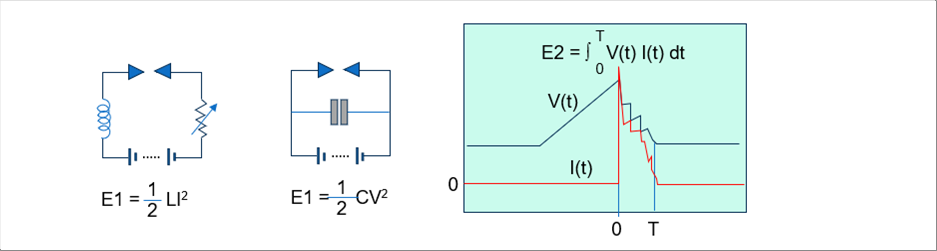左のコイルとコンデンサーの回路図の下に、エネルギーの式を表示しました。本来は、右の模式図のように、２次側の電圧と電流の積と、スパーク発生（時間０）からスパーク終了（時間T）まで合計する必要がありますが、一次側のエネルギーとほぼ同じと考えて差し支えないと思われます。
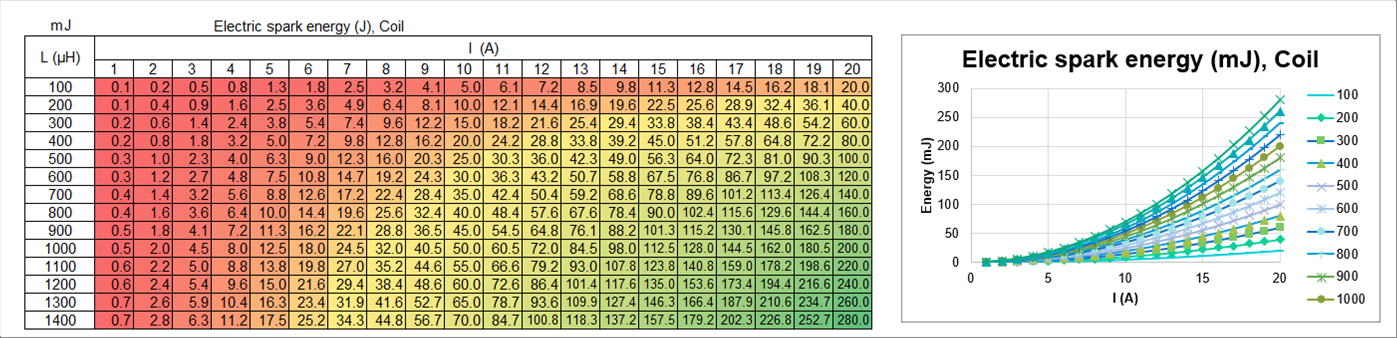
5-(3)-1 コイルのエネルギー Electric Energy of Coil
コイルのエネルギーは下の表とグラフのようになります。
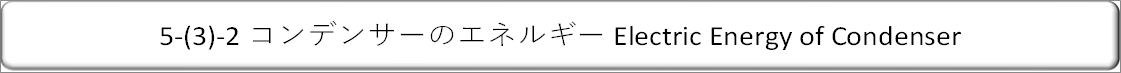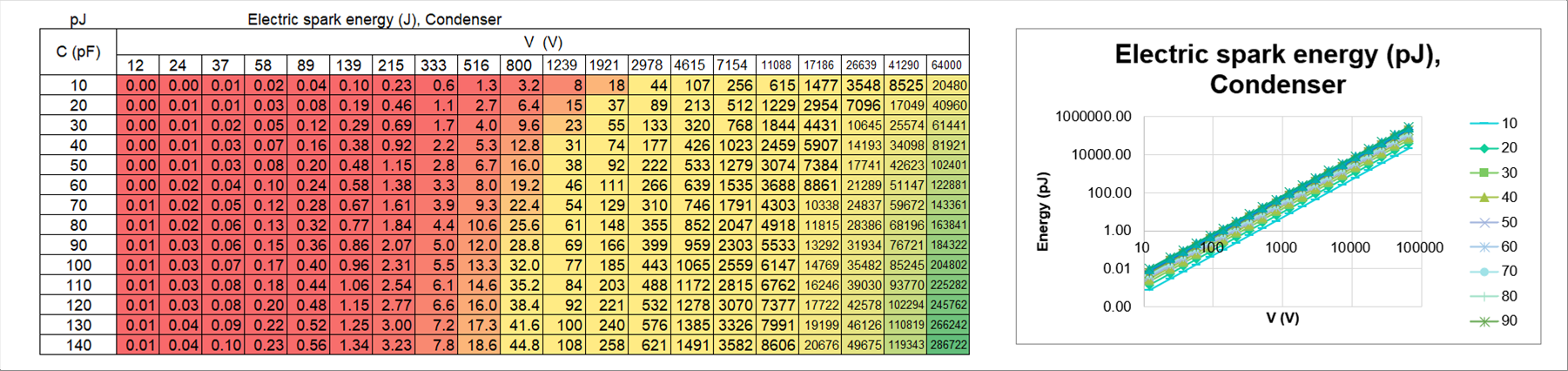
5-(3)-2 コンデンサーのエネルギー Electric Energy of Condenser
コンデンサーのエネルギーは、下の表とグラフのようになります。電圧は１２Vから６万ボルトと広範囲なので、対数グラフにしています。
5-(4) やすり式ライターの火花温度 Flint Lighter Spark Temperature
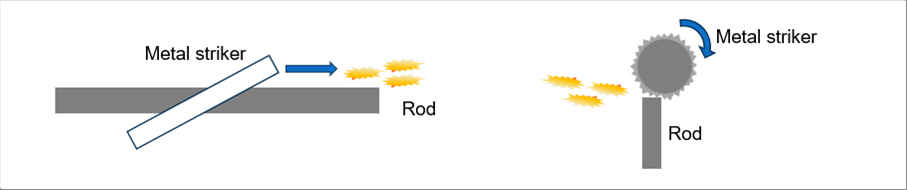
やすり式着火器具を下のイラストで示しました。左は、キャンプなどで火を起こすときに使います。ロッドと金属製のストライカーを手に持って、ストライカーをロッドの上で押しつけながらスライドさせて使います。
右は、ライターなどに見られる小さなぎざぎざ付きのホイルを回すタイプです。いずれも、こすることで火花を発生させており、この方法は、やすり式着火と呼ばれています。
最近では、左をフリント式着火と言うのが主流のようですが、フリントとは、「火打石」の意味です。ロッドが「火打石」で、と金属製のストライカーが「火打金」です。
ロッドの材質は、フェロセリウム、マグネシウムなど、融点が低く着火しやすく、かつ、燃焼温度が高いものを使っています。
フェロセリウムの火花温度は3315度C、マグネシウムの火花温度は3099度Cになります。どちらも気体燃料の着火温度は超えているので、熱流束は、臨界熱流束より大きいと思われます。十分な火花の持続時間があれば、着火可能です。
5-(5) 熱損失の原因と対策 Reasons and Countermeasures for Heat Loss
5-(5)-1 熱損失の原因 Causes of Heat Loss
十分着火する熱が得られたと思う時でも火がつきにくい時があります。これは、発生した熱量は全部を着火に使うことはできず、いろいろな理由で着火以外に取られてしまうからです。
フリント式ライターのロッド材の火炎温度は3100度Cから3300度Cです。フリント式の特徴は、ロッド材がストライカーとの摩擦で発火し、その火の粉が直接対象物に飛来して、いわば延焼する方式です。
フリント式ライターを使っても、なかなか火が付かない時があります。原因としては、湿った木材、冬の低温、吹く風などが考えられます。
気体燃料に、やすり式（フリント式）で着火する場合も同様な状況が考えられます。
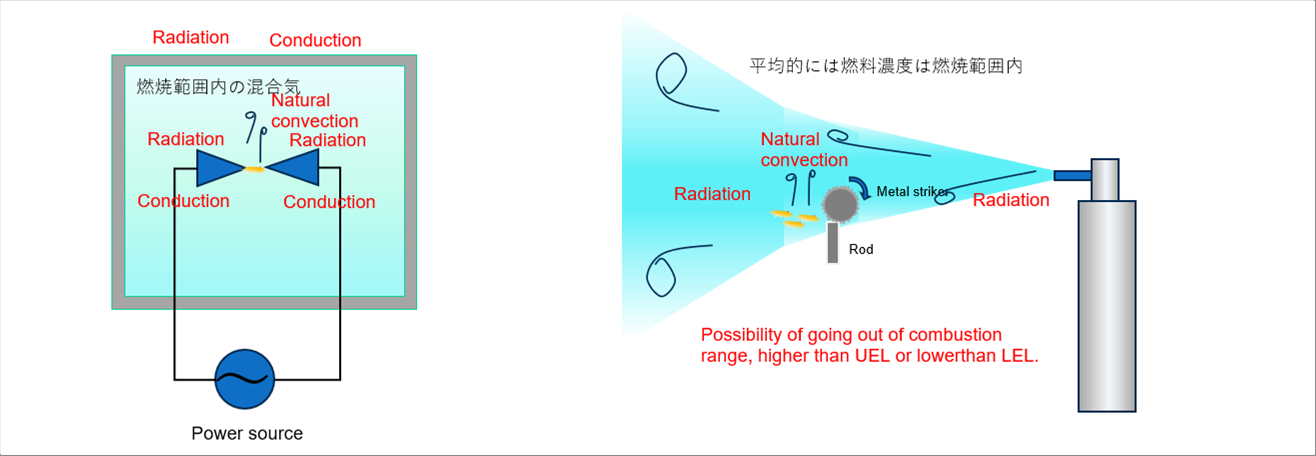
電気スパークで着火する場合は、フリント式とは様相が違います。まず、スパークから熱輻射が全周囲に放射されます。熱輻射は、絶対温度の４乗に比例して伝わるので、火花温度が高いと損失も大きくなります。輻射の一部は当たった面で一部が吸収され、残りは反射されます。この輻射熱の大きさと吸収量は熱力学的に計算できます。スパークは、混合気に自然対流を発生させます。さらに、電極を経由して着火装置に熱が逃げていきます。対流混合気が点火チャンバーの壁に到着すると、壁への伝達と壁内部での伝導で熱が逃げていきます。
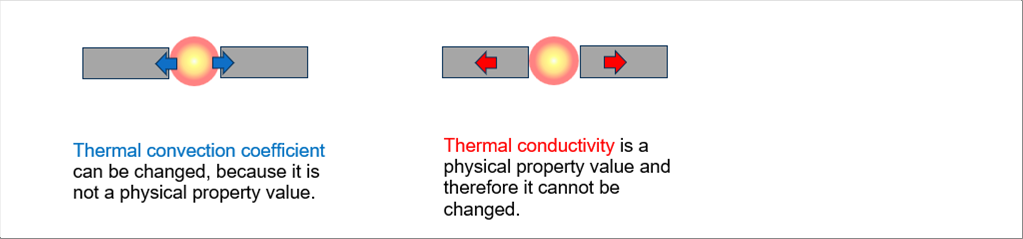
熱損失は、着火する環境の、個々の構成要素の熱伝導率と温度差の積に比例し、距離に反比例します。
各部に奪われる熱を、輻射の式、伝達の式、伝導の式で計算することも可能だと思いますが、簡単ではありません。詳細は、熱力学のそれぞれの項を参照いただきたいのですが、特に熱伝達は、熱力学と流体力学との連立方程式を解くことになります。また、燃料、空気には温度依存性もあります。こちらは数値計算で回帰式を紹介しています。境界条件としては、装置の素材、形状を使用します。
5-(5)-2 熱損失の対策 Countermeasures for Heat Loss
キャンプなどでは、ロッドを削ってたきつけ材にまぜ、そこをめがけて火花を飛ばすと、高温の火炎が発生するので、多少湿っていても火が付くと思います。ライターは風がかまう時は、ライターを手で囲ったり、背中を風上に向けてライターに風が当たらないようにするなどはよく使う手だと思います。どれも、熱力学的にも理にかなっています。
気体燃料の混合気の熱損失対策は、そのような方法は採用できませんが、熱力学的に考えなくてはいけないのは同じです。
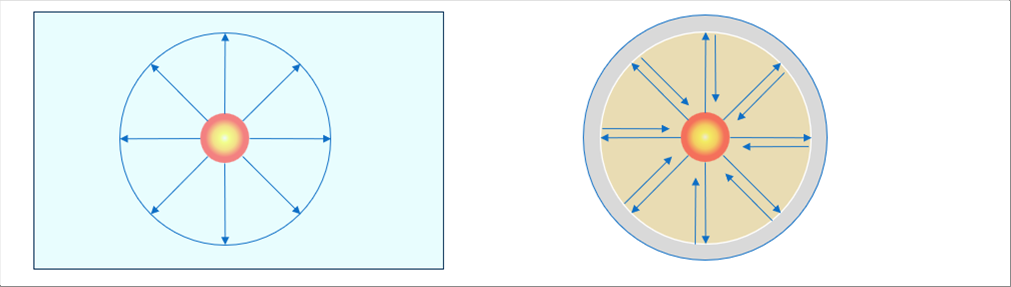
輻射は、反射板を使ってある程度跳ね返すことができます。反射板は、壁面より熱伝導率が小さいほうがいいので、発生熱で溶解しない金属を薄い耐火物に蒸着したものなどが使えれば効果があるともいます。セーブできるエネルギーは、キルヒホッフの法則で計算できます。
対流は、燃焼を狭い範囲に限れば、その範囲全体の温度があがるので、次第に小さくなるはずです。範囲を小さくできない場合は、混合気を予熱できれば同様の効果が期待できます。
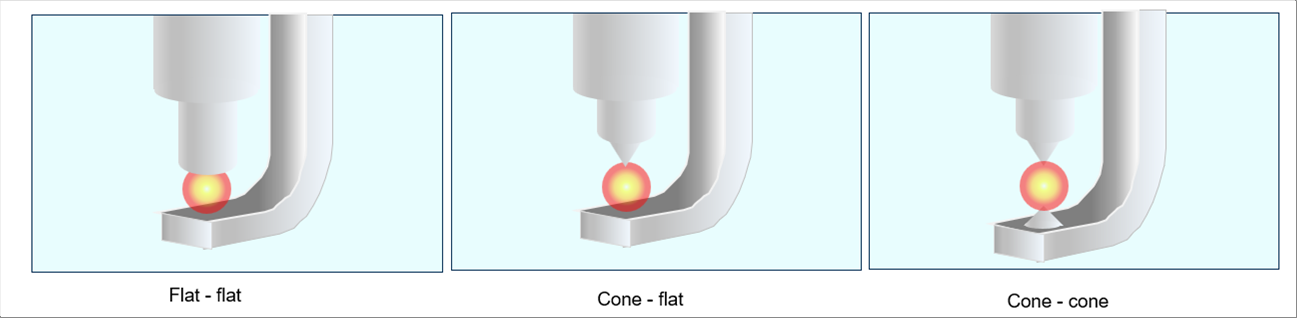
発火器具への伝達、伝導を減少されるためには、接触面を小さくするのが一番いいと思います。スパークプラグのような形状を考えるとイメージしやすいと思います。この点だけを考えるとフラットな電極より、コーンタイプの電極のほうが有利だと思います。ただし、電極の体積が小さくなるので、耐熱性がある材料を使わないと電極が解けてしまう恐れがあります。
22500
電極内部の熱伝導を小さくすると徐々に温度が上がるので熱損失は小さくなりますが、熱伝導率は物性値なので、電極の材料を決めたら変更できません。また、実際には、電極の温度が上がると電極の耐熱限界に近くなり電極が損傷する可能性があるので、逆に電極を冷却するようにしていると思います。
5-(5)-3 熱損失の想定 Assumption of Heat Loss
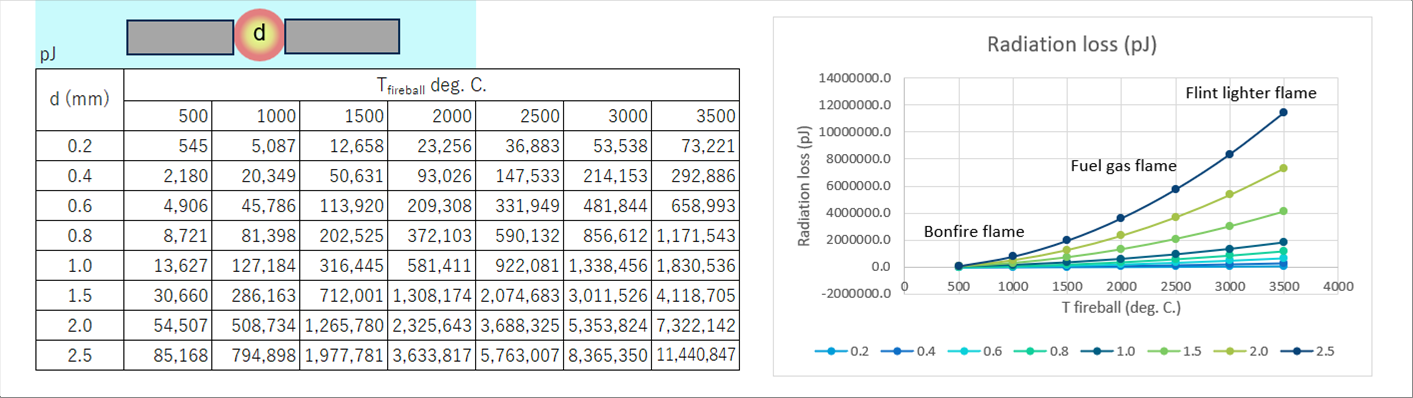
点火時の炎、スパークの温度から、放射損失を計算してみました。下の表とグラフは、火炎球の計算結果です。球の表面積が大きいために、放射損失が非常に大きいことがわかります。
5-(5)-3-a 火球の熱損失 Heat Loss of Fireball
NGK様に教えていただいたデータでは、プラグの静電容量は50pF以下とのことでしたので、電圧４万ボルトで発生熱は約42600pJです。電極間距離1mmの輻射損失は、火炎温度が2000度で約58100ｐJなので、発生熱より大きく、燃料に点火する熱は残らない計算になります。
5-(5)-3-b 電光の熱損失 Heat Loss of Lightening
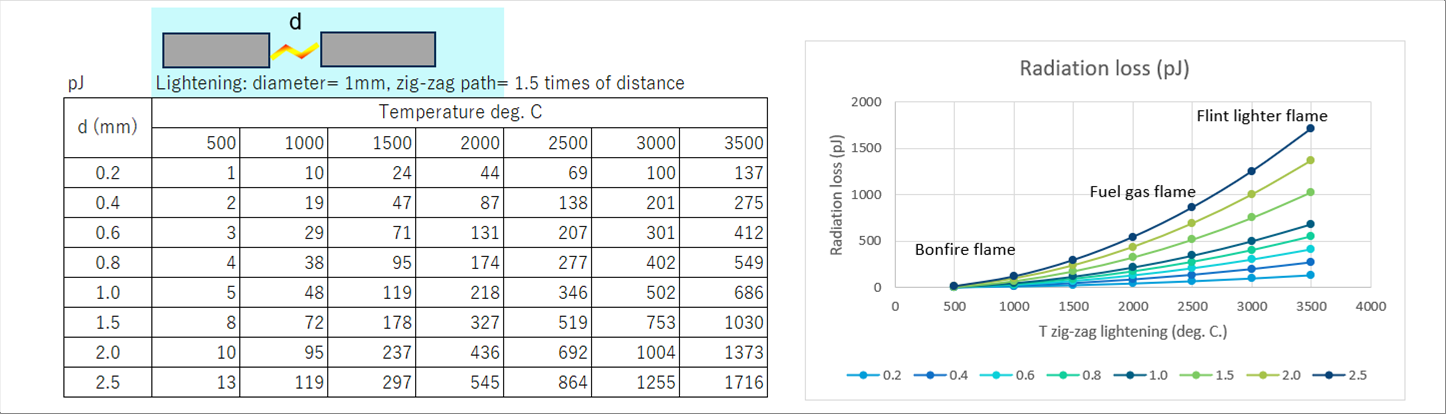
火球の計算では輻射損失を大きく見積もりすぎている可能性があるので、別の想定をしてみたいと思います。下の表とグラフは、電極間のスパークをジグザグの雷光と想定して計算したものです。雷光の断面積は円形で、電極間距離より1.5倍の長さを通ると想定した数値です。ジグザグ雷光の表面積は、火球の表面積の500分の一から7000分の１なので、放射損失は火球の場合より小さくなっています。
実際の輻射損失は、上の二つのケースの中間のどこかではないかと思われます。
熱伝達損失は、条件に合った熱伝達係数を計算する必要がありますが、割愛させていただきます。定常状態の熱伝達係数は、流体の運動方程式と熱の式の連立方程式にして解析的に解けますが、点火は非定常状態なので、たぶん解析的には解けないと思われるからです。
5-(5)-3-c 電極への伝達損失 Convection Loss to Electrodes
電光もしくは火球が電極に達すると、電極への熱伝達が発生します。
熱伝達量の計算には熱伝達係数を計算する必要がありますが、火球、電光のどちらも境界条件を推測することは（筆者には）きわめて困難です。「熱力学基礎」に、レイノズル数と熱伝達係数の範囲をのせましたが、一般的には自然体対流で数W/m2K、強制対流で数十から数百W/m2Kレベルといわれています。
最小着火エネルギーがミリジュール、電気スパークのエネルギーがピコジュールなので、伝達係数は３桁から１２桁大きいことになります。
電気スパークのエネルギーは、電極に到達すると電極にほぼすべて吸収され、電極の温度を上げるために使われると推測されます。熱伝達係数=1 W/m2K、温度差が0.5度Cまでの伝達損失を下の表とグラフに示します。
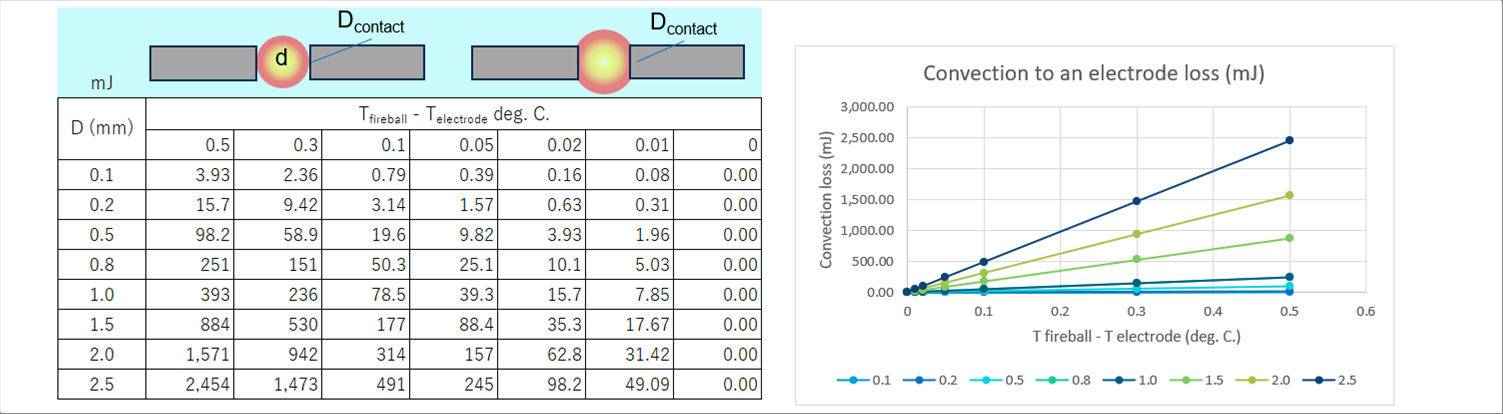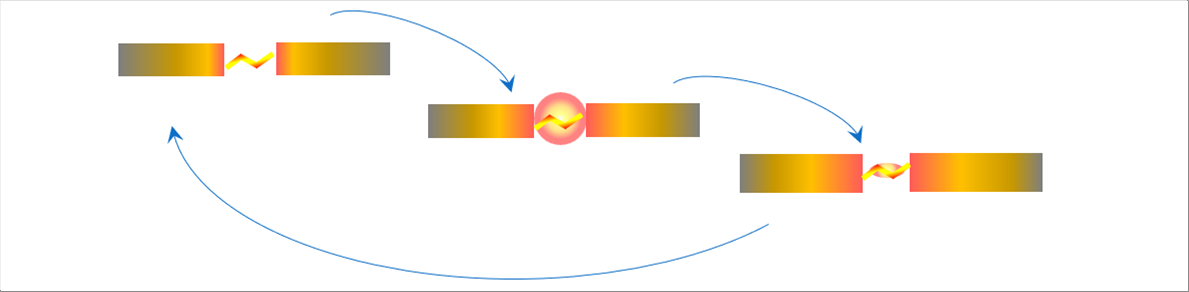
5-(5)-3-d 失火の可能性 Possibility of Misfire
ジグザグ雷光では、接触面積が小さいので電極への熱伝達も小さく、混合気に点火できるのではないかと推測されますが、点火された混合気は爆発して火球になると思われます。火球の温度は5-(2)火炎温度にあるように2000度Cレベルなので、輻射損失が激増し、かつ、電極への熱伝達面積が大きくなるため、熱伝達損失も急増します。燃焼継続に必要なエネルギーは最小着火エネルギーを同じと考えられるため、燃焼を継続できなくなる可能性が非常に高く、失火する可能性が大だと思われます。
下の模式図は、雷光型スパーク、混合気の火球発生、同消滅を模式的に描いたものです。
熱損失としてどのくらいが適切か、正直言ってよくわかりませんが、火炎球の損失とジグザグ雷光の損失の平均程度だとすると、発生エネルギーの約50%が輻射損失と推測されます。伝達損失が20%だと仮定すると、合計70%が損失となります。この数値は、ある程度経験のある方を入れて、関係者で事前に同意しておくのがいいと思います。
損失は、炉の大きさ、着火器具、着火材、使用燃料などで変わるため、炉の修理の後はいつも点火しにくいなど、経験者の方は貴重な経験をお持ちです。
Author: T. Oda
このページはエクセルで作り、excel2webでhtmlとcssを自動作成しました。