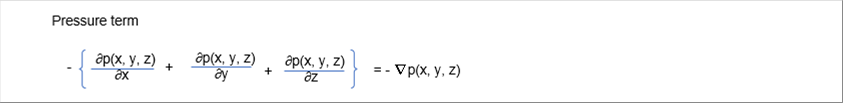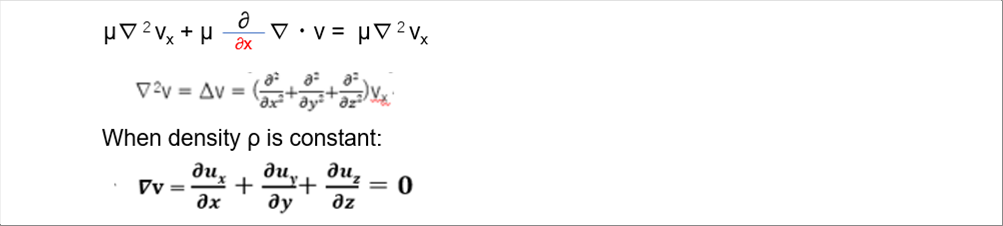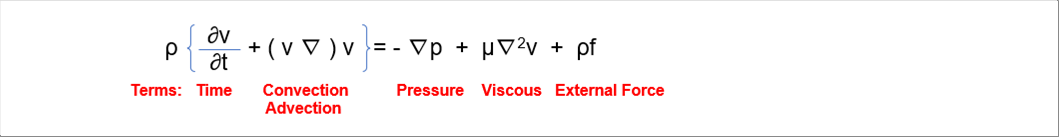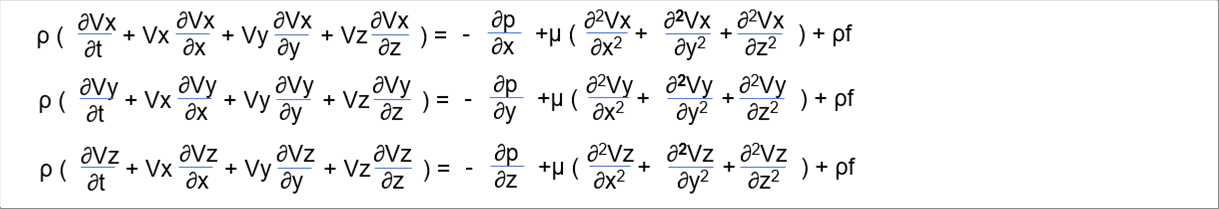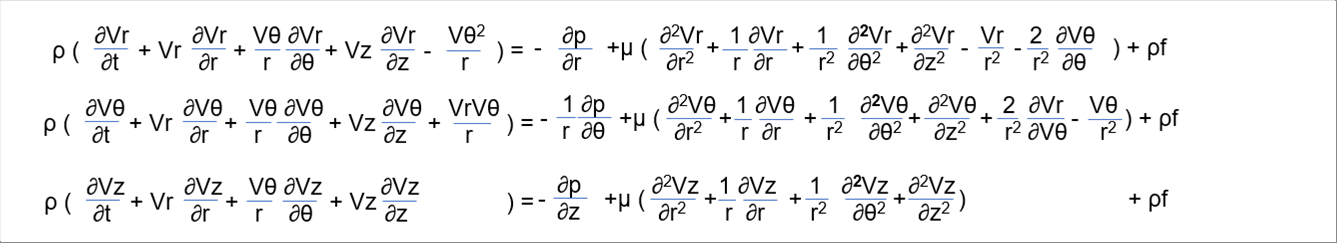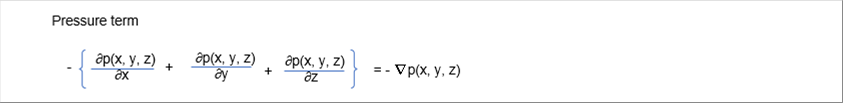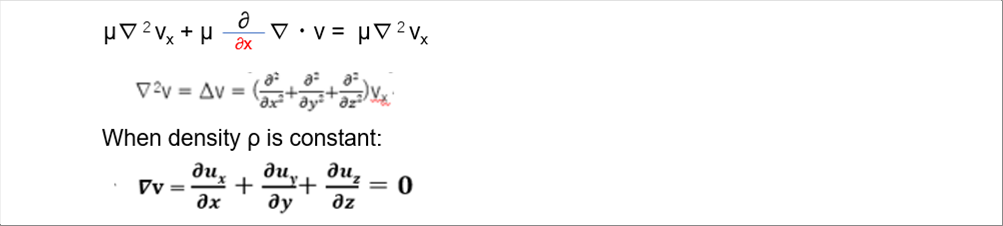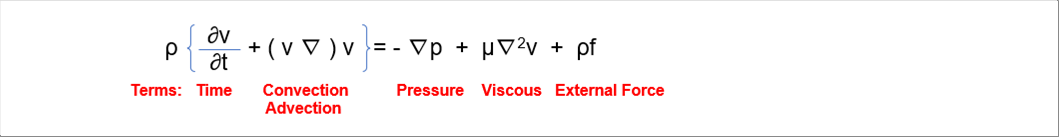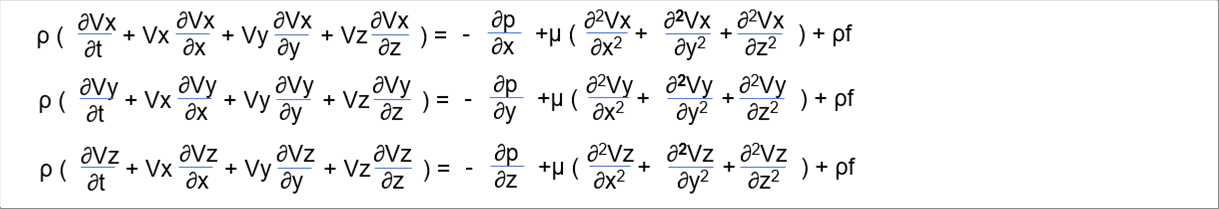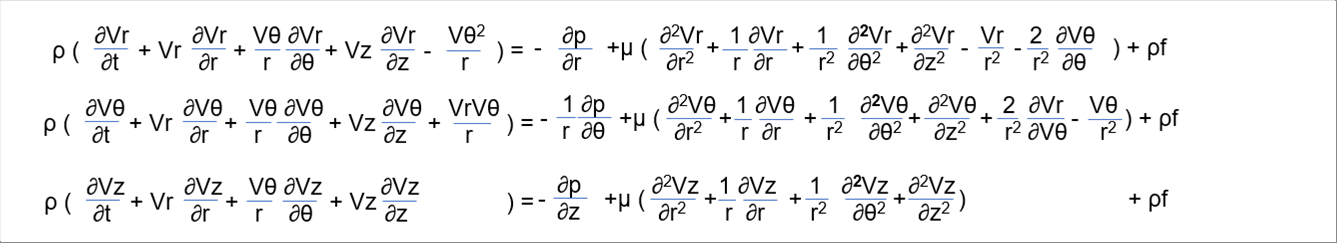| |
 |
| |
 |
| 1 Navier-Stokes Equation |
| 2 Time Term and Convection (Advection) Term |
| 2-(1) Meaning of Material Derivative |
| 2-(2) Derivation of Material Derivative |
| 3 Pressure Term |
| 4 Viscous Term |
| 5 External Force Term |
| 6 Equation of Motion |
| 6-(1) Navier-Stokes Equation (Cartesian Coordinate Components) |
| 6-(2) Navier-Stokes Equation (Cylindrical Coordinate Components) |
| |
 |
| 1 Navier-Stokes Equation |
| |
| The Navier-Stokes equation, which is the equation of motion of fluid, is given as follows. Although it looks more complex than the equation of moti0n of an object, which consists only of the time time on the left side and the external force term on the right side. The equation of mothion of fluied needs only three (3) additional terms: convection (advection), pressure, and viscous terms. The author wuld like to explain each of them in turn. |
| |
 |
| |
 |
| 2 Time Term and Convection (Advection) Term |
| |
 |
| 2-(1) Meaning of Material Derivative |
| |
| The author would like to explain the material derivative for the consideration of the convection (advection) term. The equation of motion of a solid object describes its change over time from the fixed viewpoint. It is said that Newton came up with the equation of motion when he say an apple fruit falling from an apple tree without moving. Since the time derivative of the position is velocity and the time derivative of velocity is acceleration, acceleration is the second-order derivative of position. In the equation of motion of a fluid, the perspective flow with the fluid. From that point of view, the temporal changes of the surrounding objects (including fluid) are observed. Because fluids are continuums, it is not only their positions that change over time but also the incoming and outgoing flows of the surroundings to the place being observed. In incompressible fluids, the density is constant, but its contents change. In compressible fluids, the density also changes. In this way, "differentiation along an object" is called "material derivative". |
| |
 |
| 2-(2) Derivation of Material Derivative |
| |
| Even if the flow is stationary, when a material with a different temperature enters it, it will flow by convection. If the temperature is exactly same, the convection term is zero (0) in the stationary fluid. |
| |
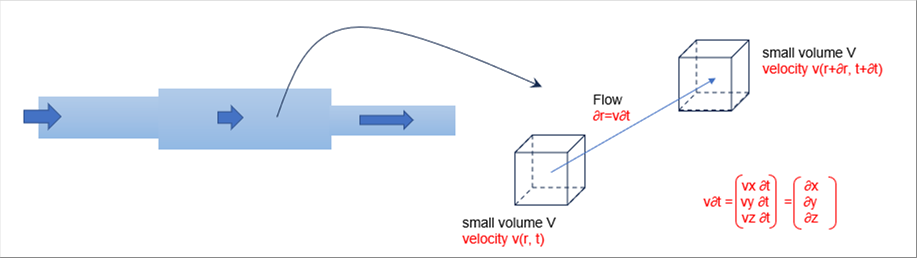
| As shown in the following picture, let's consider a microscopic volume somewhere in the flow path where the cross-sectional area changes in the middle. |
| |
| |
 |
| |
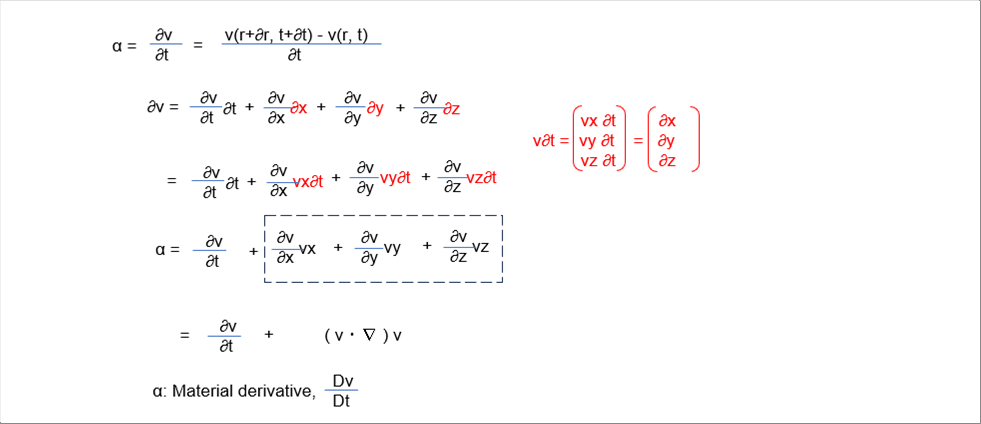
| Suppose that the minute volume in the left is moving along the flow. We may follow the equation of motion of a solid for the consideration of equation of motion of fluid. Since acceleration is the time derivative of velocity, it is given by: |
| |
 |
| |
| The first term is called the time term and the second one is called the convection (advection) term. Now we have obtained the derivative of the velocity from the point of view of moving along the flow of fluid. Since we have "differentiated the velocity along the material," we call is the material derivative. The Nabla operator is a simple sum of first-order derivative. The advantage of using this symbol is that we can use the same formula to other coordinate systems such as cylindrical coordinate system. |
| |
 |
| 3 Pressure Term |
| |
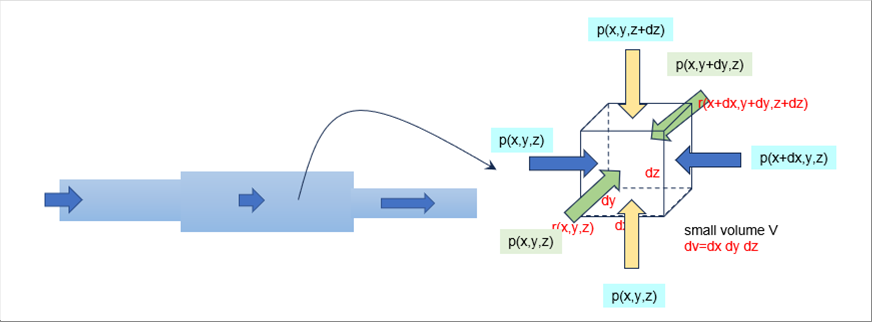
| Next, let's consider the pressure term. The following pictures show the force equilibrium in the microscopic volume V. |
| |
 |
| |
| The force equilibrium in the x-axis direction is as follows. |
| |
 |
| |
| Since the sign is negative, when the pressure is the direction becomes lower, it will flow in the direction, but if the pressure in the direction of travel becomes higher, it will flow in the opposite direction. |
| |
| The y and z directions can be calculated in the same way, resulting in the pressure gradient in each direction. As a summary, the pressure term is given by: |
| |
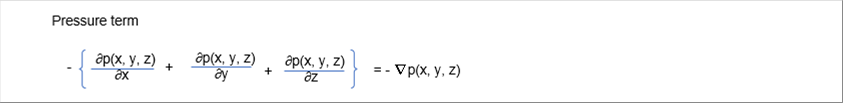 |
| |
| |
 |
| 4 Viscous Term |
| |
| For details, please see "Basis of Fluid Mechanics", but the flow velocity of a fluid is communicated sequentially by viscosity. The following picture shows the two (2) layers next to each other. |
| |
 |
| |
| It can be assumed that the fast layer is pulling the slow one, and conversely, the slow one is braking the fast one. The pulling (braking) force is called shear force, and it is considered that the shear force is generated by the velocity difference. The shear force is assumed proportional to the velocity difference, and the proportionality coefficient is called viscosity (viscosity coefficient). This is called Newton's law of viscosity. |
| |
 |
| |
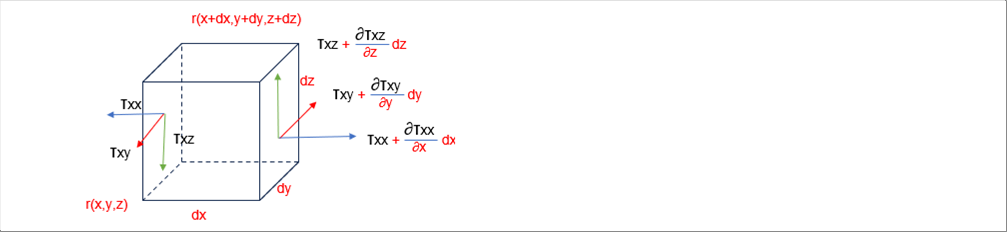
| The shear force acting on a microscopic volume is shown in the picture below. |
| |
 |
| |
| The sum of the shear force in x direction is given by: |
| |
 |
| |
| The viscous force applied to the microscopic volume dxdydz is in the blankets ( ) in the above equation. Substituging Newton's law into the shear force, the blankets ( ) is giben by: |
| |
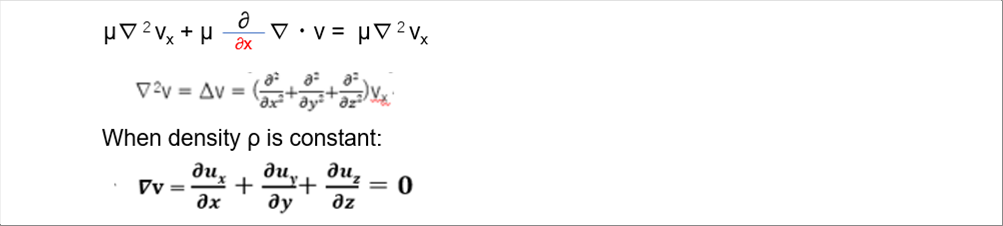 |
| |
| The last line of the above equations shows that if the density is constant, the Nabla v is zero (0). This is called the formula of continuity of incompressible fluids. It explains that the velocity change in a direction is compensated by the other directions. |
| |
| Since the same holds true in the y and z directions, the following equation holds true. It is callded the viscous term. |
| |
 |
| |
 |
| 5 External Force Term |
| |
| The external force term is what of the force applied to the fluid. It is like the equation of motion of a solid object. |
| |
| The external forces are not shear forces acting between adjacent fluids, but environmental (?) one. Besides gravity, centrifugal force, buoyancy, surface tension, etc. can be the ones. |
| |
 |
| 6 Equation of Motion |
| |
| When a force acts on an object, its velocity changes. This is expressed in the equation, the product of the mass m of object and the acceleration alpha is equal to the external force F. |
| |
 |
| |
| Substituting the terms obtained so far into the above equation and dividing both sides by the volume, we get the Navier-Stokes equation. |
| |
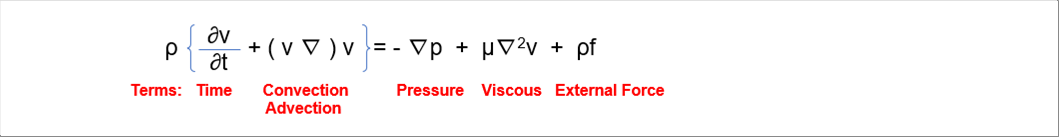 |
| |
 |
| 6-(1) Navier-Stokes Equation (Cartesian Coordinate Components) |
| |
| The following equations show the components of the Navier-Stokes equation in Cartesian coordinate system. |
| |
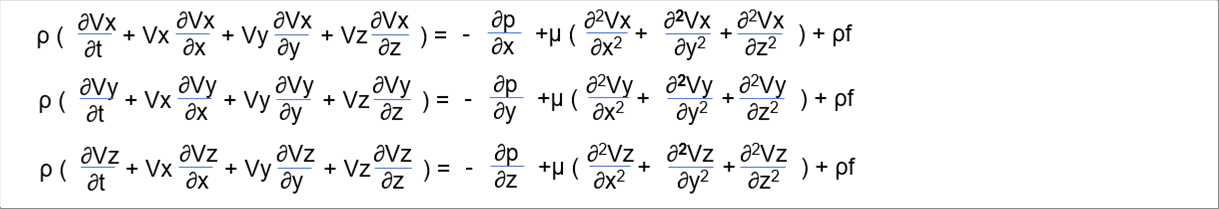 |
| |
 |
| 6-(2) Navier-Stokes Equation (Cylindrical Coordinate Components) |
| |
| The following equations show the components of the Navier-Stokes equation in cylindrical coordinate system. |
| |
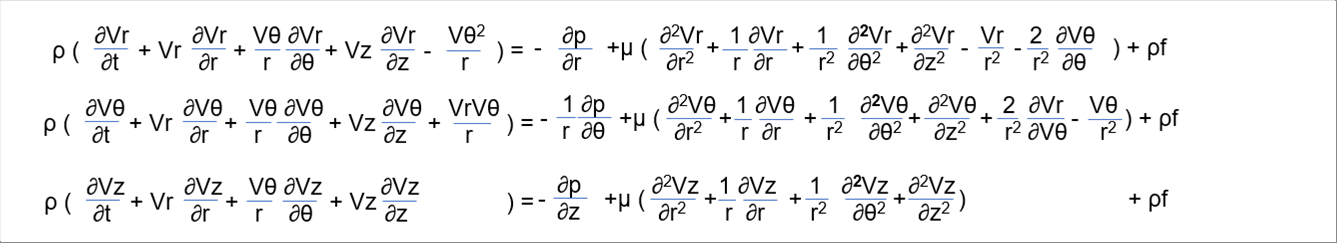 |
| |
| |
| |
| Author: T. Oda |
| The page was prepared in Excel, and html and css files were automatically generated by the excel2web. |