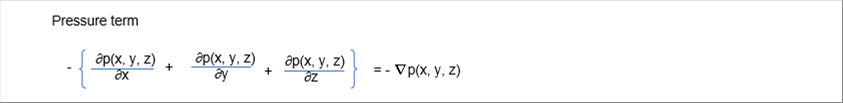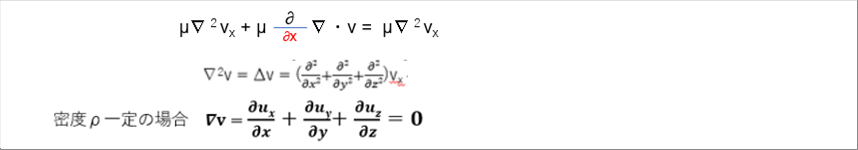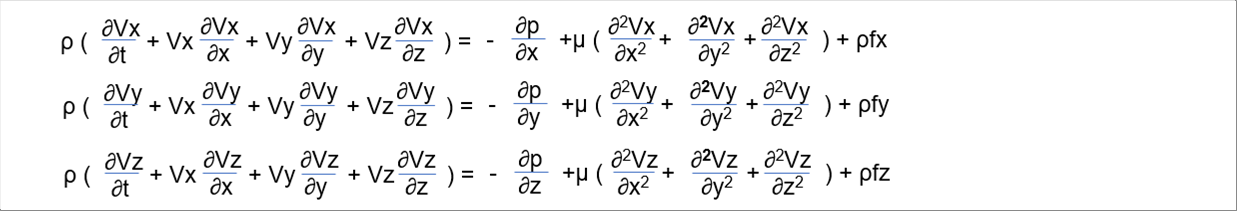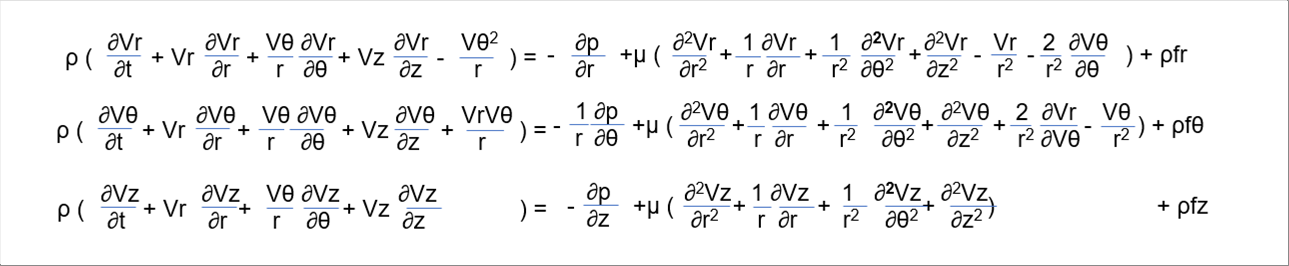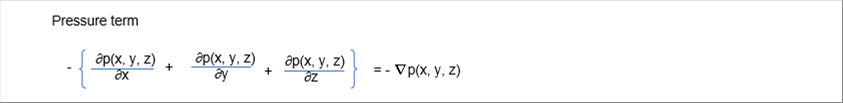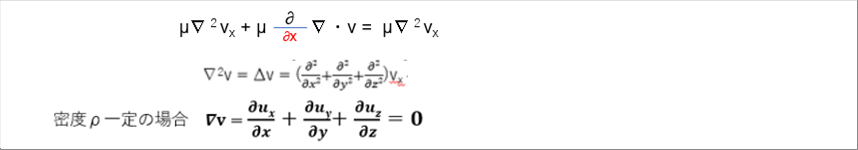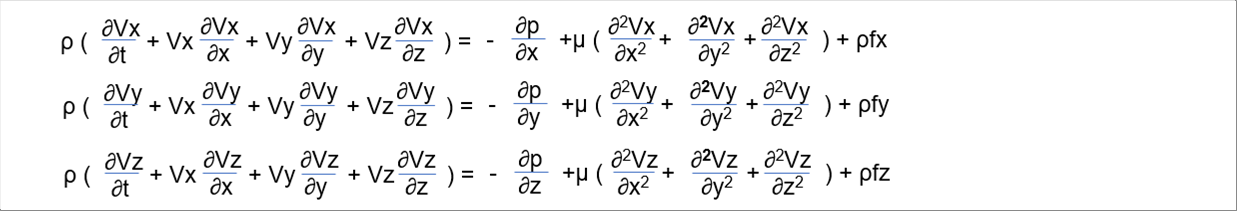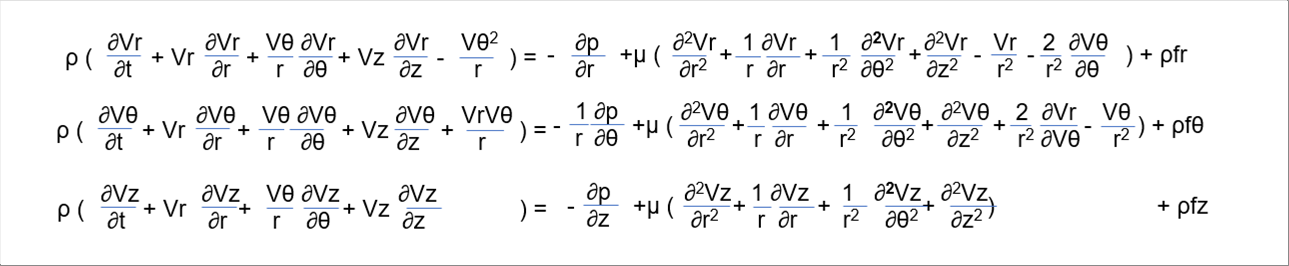| |
 |
| |
 |
| ● ナビエ・ストークス方程式 |
| ● 時間項、移流項 |
| 〇 物質微分の意味 |
| 〇 物質微分の導出 |
| ● 圧力項 |
| ● 粘性項 |
| ● 外力項 |
| ● 運動方程式 |
| 〇 ナビエ・ストークス方程式 (直交座標成分) |
| 〇 ナビエ・ストークス方程式 (円柱座標成分) |
| |
 |
| ● ナビエ・ストークス方程式 |
| |
| 流体の運動方程式であるナビエ・ストークス方程式は、次式で与えられます。物体の運動方程式よりずいぶん複雑に見えますが、物体の運動方程式は、左辺の時間項と、右辺の外力項だけでできています。流体の運動方程式は、それに加えて対流項、圧力項、粘性項の3項が追加されているだけです。それぞれ、順番に見ていきたいと思います。 |
| |
 |
| |
 |
| ● 時間項、移流項 |
| |
 |
| 〇 物質微分の意味 |
| |
| 移流項を考えるにあたり、物質微分について説明させてください。固体の運動方程式は、ある場所から固体を観察して、その時間変化を表しています。ニュートンは、自分は動かず、リンゴの木から落ちるリンゴの実を見て運動方程式を思いついたと、言われています。位置の時間微分が速度で、速度の時間微分が加速度なので、加速度は、位置の2階微分となります。流体の運動方程式は、流体とともに流れる視点から、周りの流体の時間変化を表しています。流体は連続体なので、時間とともに変化するのは、位置だけではありません。観測しているところへと周囲で流入、流出があります。非圧縮性流体では密度は一定ですが、その中身が変わります。圧縮性流体では、密度も変化します。このように、「物体に沿って微分」することを「物質微分」といいます。 |
| |
 |
| 〇 物質微分の導出 |
| |
| 移流項は対流項とも言います。流れが静止していても、その中に温度が違う物質が入ると対流で流れが生じます。厳密に温度が同じであれば静止流体中では移流項はゼロになります。 |
| |
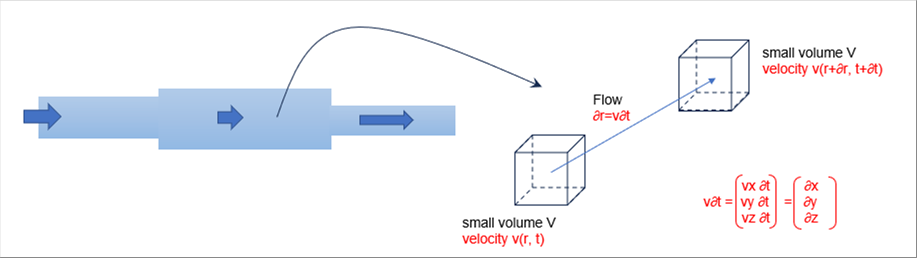
| 下の絵のように、断面積が途中で変わる流路のどこかの小体積を考えてみたいと思います。 |
| |
| |
 |
| |
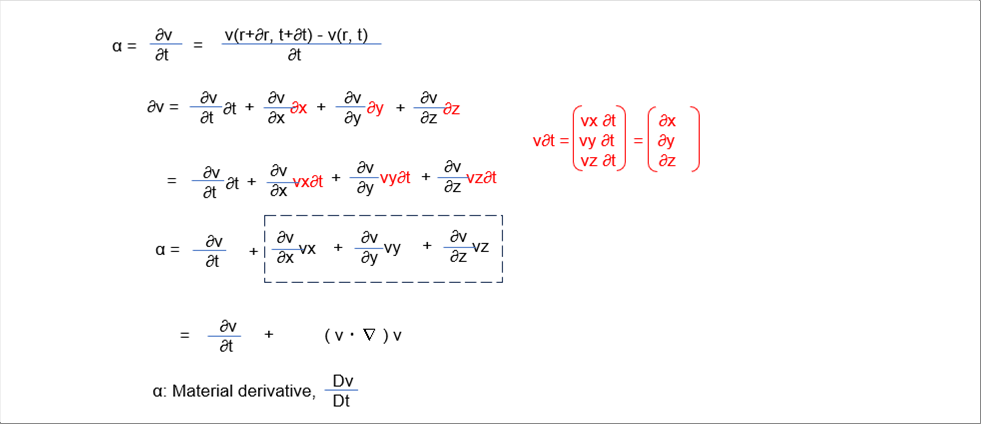
| 左手前の微小体積が、流れに沿って移動しているとします。固体の運動方程式にならって、流体の運動方程式を考えます。加速度は、速度の時間微分なので、次式で与えられます。 |
| |
 |
| |
| 物質微分の第一項を時間項、第2項を移流項(対流項)と言います。これで、流体の流れに沿って動いている視点から見た速度の微分が求められました。速度を「物体に沿って微分」したので、物質微分と言います。ナブラ演算子は、1次の単純和です。この記号で表記すると、円柱座標系を使っても同じ式で表現できます。 |
| |
 |
| ● 圧力項 |
| |
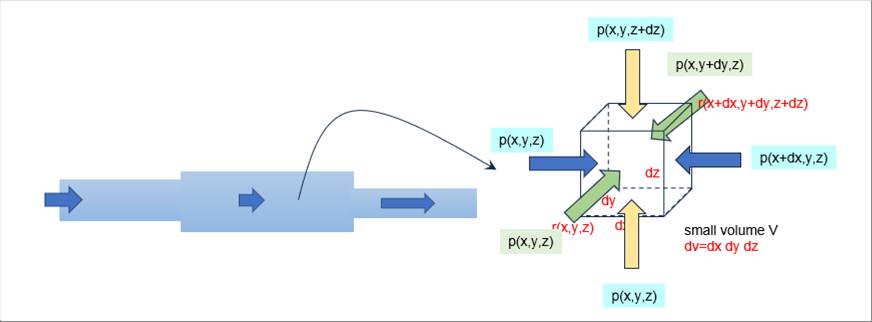
| 次に、圧力項を考えます。下の絵のように、微小体積Vの力のつり合いを考えます。 |
| |
 |
| |
| x軸方向の力のつり合いは下記のとおりです。 |
| |
 |
| 符号はマイナスになので、進行方向の圧力が低ければそちらに流れますが、進行方向の圧力が高ければ逆に流れることを示唆しています。 |
| |
| y方向、z方向も同様に計算でき、それぞれ、y方向の圧力勾配、z方向の圧力勾配になります。まとめると圧力項は次式で与えられます。 |
| |
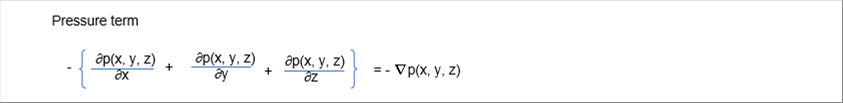 |
| |
| |
 |
| ● 粘性項 |
| |
| 詳細は、「流体力学の基礎」を参照していただきたいのですが、流体の流れ速度は、粘性によって順に伝えられます。隣り合う2層を想定すると下の絵のようになります。 |
| |
 |
| |
| この絵のように、速い層が遅い層を引っ張っていると考えられ、逆に、遅い層は速い層にブレーキをかけていると想定できます。この力をせん断力いい、せん断力は速度差によって発生していると考えれられます。せん断力は、速度差に比例すると仮定し、この比例定数を粘度(もしくは粘性係数)といいます。これは、ニュートンの粘性法則とよばれるものです。 |
| |
| ● τ=μ du/dy [Pa s パスカル秒] |
| |
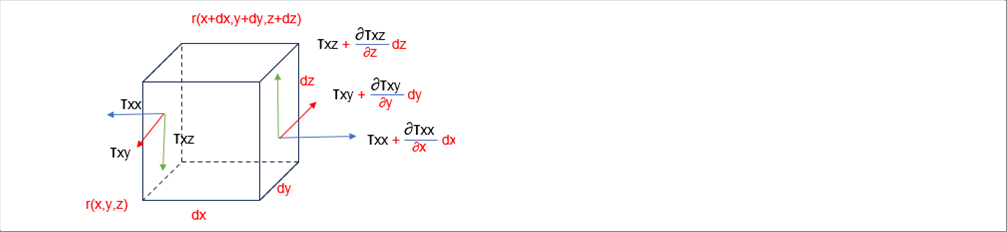
| 微小体積に働くせん断力は、下の絵のようになります。 |
| |
 |
| |
| x方向に働くせん断力の合計は次式で与えられます。 |
| |
 |
| |
| 微小体積dxdydzにかかる粘性力は、上の式の( )内になります。せん断力に、ニュートンの粘性法則を代入して整理すると、( )内は次式で与えられます。 |
| |
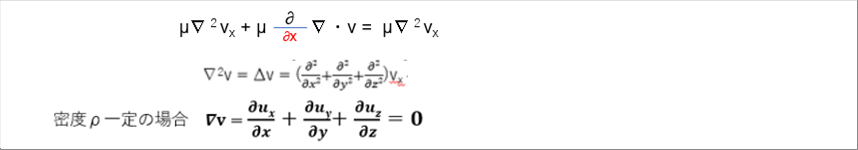 |
| |
| 3行目の式は、密度一定の場合、ナブラv(速度の単純1階微分和)はゼロです。これは、非圧縮性流体の連続の式と呼ばれています。意味合いは、ある方向の速度変化分は、ほかの方向から補給されるという意味です。詳細は、「流体の運動方程式」を参照ください。 |
| |
| 同じことがy方向、z方向でも成り立ちますので、微小体積全体では次式が成り立ち、これを粘性項といいます。 |
| |
 |
| |
 |
| ● 外力項 |
| |
| 外力項は、物体の運動方程式同様、流体にかかかる力の項です。 |
| |
| 隣り合う流体との間に働くせん断力などではなく、重力などの環境(?)の力です。重力のほかには、遠心力、浮力、表面張力などが考えられます。 |
| |
 |
| ● 運動方程式 |
| |
| 物質に力が作用すると、その物質の速度が変化することを運動方程式で表現すると、物質の質量 m と加速度 α の積は、外から作用する力 F に等しいとなります。 |
| |
 |
| |
| これまでに得られた項を、この式に代入して、両辺を体積で除算すると、ナビエ・ストークス方程式が得られます。 |
| |
 |
| |
 |
| 〇 ナビエ・ストークス方程式 (直交座標成分) |
| |
| 次式は、直交座標でのナビエ・ストークス方程式の成分です。 |
| |
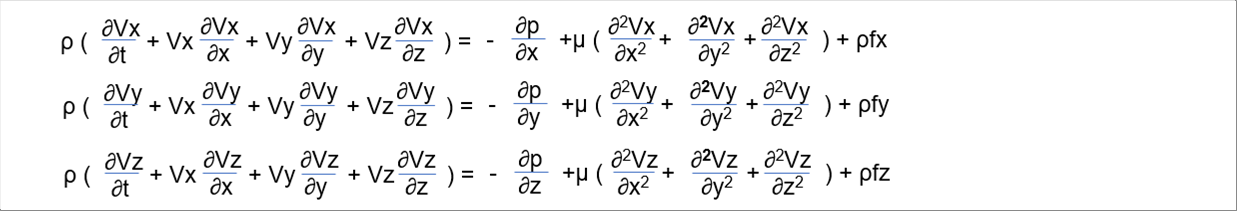 |
| |
 |
| 〇 ナビエ・ストークス方程式 (円柱座標成分) |
| |
| 次式は、円柱座標でのナビエ・ストークス方程式の成分です。 |
| |
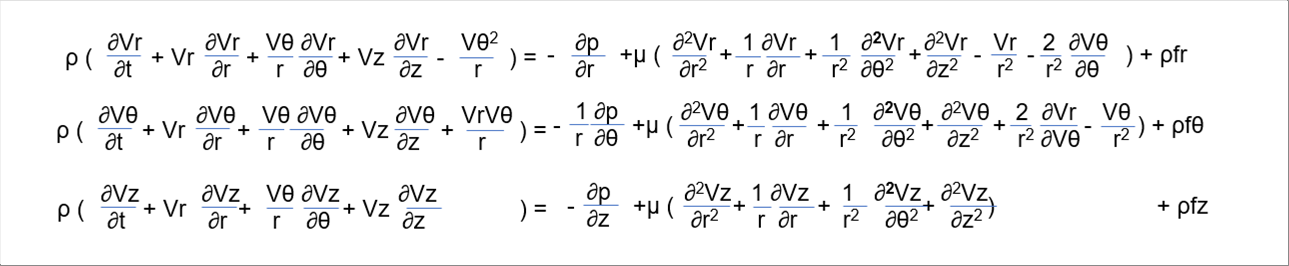 |
| |
| Author: T. Oda |
| このページはエクセルで作り、excel2webでhtmlとcssを自動作成しました。 |