材料力学　基礎
●　材料力学とは
工場関連の例
●　静荷重と動荷重
●　鋼の応力ひずみ線図
●　剛性
●　曲げ強さ　断面二次モーメントと断面係数
（１）　断面二次モーメントって何？
（２）　断面係数って何？
●　曲げ強さ　断面二次モーメント　I　の定義式
（１）　定義式
●　曲げ強さ　断面係数
●　たわみ量δ　の計算
●　応力集中とは何でしょうか。
●　クリープ、疲労
●　熱応力
●　座屈
●　材料力学とは
力学とは、物体に働く力と、その力によって物体がどう動くかの関係を知るものです。工業的には、丈夫で軽量なものを作ることが重要で、このためには、力がかかって動く量を知ることが大事になります。
これが材料力学で、物体に力が加わったときにどのように変形するか、それが壊れるのか壊れないのかを知るために発達したといわれています。
物に力が働いた場合に、壊れないようにするためにはどうしたらいいか、もしくは、物が壊れてしまった場合、何が原因だったのかを調べる場合にも使われます。
我々の大先輩は、物体の基礎的な微分方程式を積分して力と動き量の関係を導出されました。したがって、公式を暗記していなくても、小さな領域の力のつり合いの微分方程式を解けば、同じようにが計算できます。単純な構造のものは公式をそのままあてはめればいいですが、複雑な形状のものは有限要素法などを用いることができます。
筆者が大学の時に教えてもらった「自然界は単純である」ということは材料力学にも適用でき、そのものの本質に注目し、細かい点は無視して簡易解を求めることも重要になります。
〇　工場関連の例
工具設計：バー、キャップ、ホルダーなど
弾性変形補正：ロータリ―矯正、プレスなど
安全装備設計：歩廊、階段、手すりなどが壊れないようにするなど
材料力学では、物が変形したらそれを補正する、物が壊れないようにすることが重要ですが、物が壊れることを有意義に使うと、素材形状とは違った形状で高強度な別のものを得ることができます。これは、塑性加工の分野になります。
●　静荷重と動荷重
物体にかかる力は、机の上に置かれたリンゴなどの静荷重と、ホームランを打った時のような動荷重に大別されます。動荷重は、繰り返しかかる場合があり、さらに、ゼロからプラスなのか、マイナスからプラスなのかでいくつかに分類されます。釘打ちは、ゼロからプラス方向のみの繰り返し荷重、車のエンジンの振動などは、体が左右逆方向に振られるので、プラスとマイナスの繰り返し荷重といえると思います。
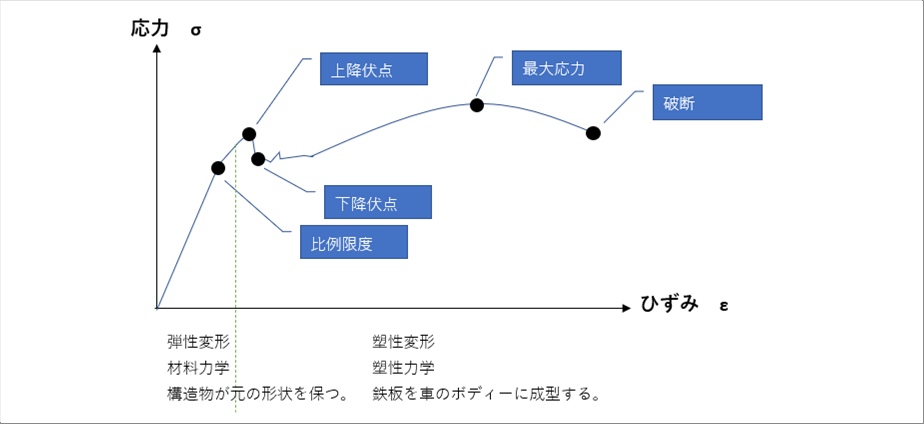
●　鋼の応力ひずみ線図
応力とひずみをグラフにしたもので、材料力学の基礎になるものです。
材料力学は、材料が変形しても元に戻る弾性変形の範囲で考えるので、応力ひずみ線図のゼロ点から弾性限度までの範囲を考えます。
力を変形量で割った数値を剛性といい、力が同じで、変形量が小さいとこの剛性は大きくなります。つまり、剛性が大きいと、変形しにくいことを意味しています。
物体にかかる力は、物体と同じ方向にかかる場合、物体と垂直にかかる場合があります。物体にかかるモーメントは、物体を曲げるようにかかる場合と、ねじるようにかかる場合ががあります。したがって、物体にかかる力と変形は、４種類になります。実際には、この４つが全部同時にかかっている場合もあります。
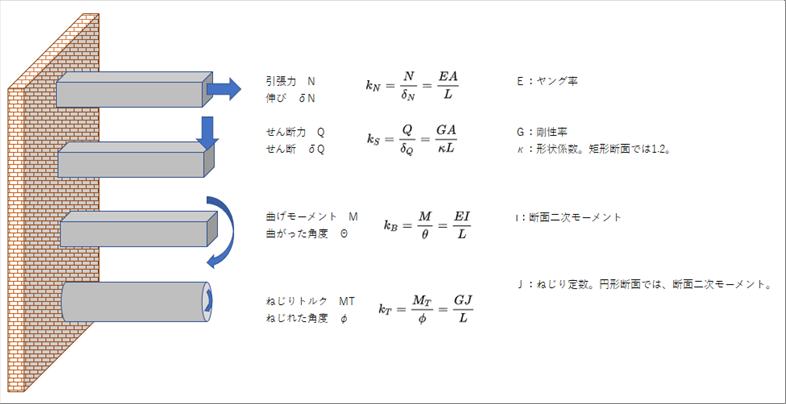A：物体の断面積
L：物体の長さ
N：物体にかかる力
δN：Nによって伸びた長さ
M：物体にかかるモーメント
Θ：Mによって物体が曲がった角度
Q：物体に垂直にかかる力
δQ：Qによって物体がQ方向に変形した長さ（せん断）
MT：物体をねじる力（トルク）
φ：MTによってねじれた角度
式の最初の項が剛性の定義です。物体にかかる力と、その方向の変形量が計測できれば剛性はわかりますが、その物体を作る前には、力をかけられませんし、変形量もわかりません。ひょっとするとその力によって破壊されてしますかもしれません。
材料力学では、その物体を作る前に、どのくらいの力がかかるとどのくらいの変形量になるかを知ることが重要です。それができれば、変形量が許容範囲に収まるようにどういう材質、寸法を決めることができます。
剛性の定義式から、変形量をなくしたものが式の２項目目です。ヤング率は使う物質によって一定値（物性値）なので、文献でわかります。断面二次モーメントは、部材の寸法で計算できます。こちらの式だと、使う材質と部材の寸法がわかれば剛性がわかるので、どのような力がかかったらどのくらい変形するかが容易に計算できます。
急に「断面二次モーメント」が出てきましたが、物体の断面のモーメントに関係する数値なんだくらいの軽い気持ちで見ていてください。次で説明したいと思います。
部材がどこで使われているかも加味した、曲げにくさを表し、数値が大きいほど曲げにくいとこを示しています。これは、断面の形状に、どこで使われているかの位置情報でできています。同じ部材でも、曲げたくないところから離して使うほうが断面二次モーメントが大きくできるので、曲がりにくくなります。見栄えや設置可能位置の製薬の範囲で、どこに使うかでかで、より曲がりにくくできます。具体的にどれだけ曲がるか（たわみ量）も計算可能です。部材を使う場所での断面二次モーメントは、部材の図心を原点にした数値に、使用位置と断面積の積を加算した数値で定義されます。
断面二次モーメントは、どこで使うかによって数値が変わりますが、断面係数は、使う位置は関係ありません。断面係数は、文字通り「断面」自体の性能を表す「係数」で、図芯を通る断面に似モーメントを、応力を知りたい位置で割り算します。部材の応力を計算するときに使われ、図芯からの距離で割るので、部材の表面の応力が最大値になります。このため、断面係数は、図芯から表面までの距離で割ったものが使われます。
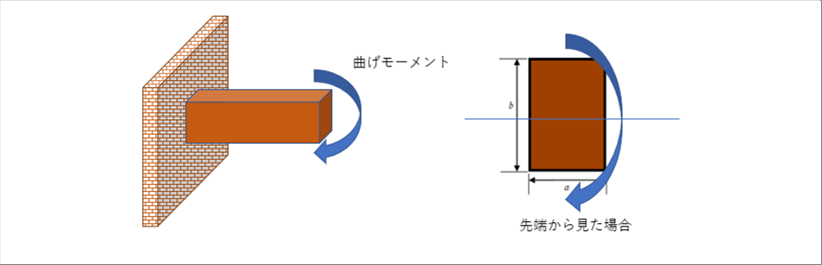
断面二次モーメントは、部材の曲げにくさを表し、数値が大きいほど曲げにくいことを意味しています。断面二次モーメントは、たわみ量の計算に使われることが多いです。
（１）　定義式
断面の形状がどのようであれ、図芯からある位置の部材の寸法の二乗を部材の面積で積分した値になります。
モーメントがかかる方向の寸法をｈ（上ではｂ）、他方をｂ（上ではa）と書くことがおおいので、それに従うと、四角形、円形、円筒形の断面係数は
四角形 Ix = bh^3/12
円形　Ix = πd^4 / 64
円筒形 Ix = π（do^4 - di^4) / 64
●　曲げ強さ　断面係数
断面係数：部材の断面性能を表す係数で、曲げる力に対する強さ、抵抗性を示す。
断面係数　Z = I/y　に、 表面位置 y=h/2 (d/2)を代入する。
長方形　　Z = bh^2/6
円形　　 Z = πd^3/32
円筒形　 Z = 0.0982(d^4-d1^4)/d
●　たわみ量δ　の計算
たわみ角Θ＝曲げモーメントを1回積分
たわみ量δ＝曲げモーメントを２回積分
たわみの式は、加速度の１回積分が速度、２回積分が位置になるのと似ている。
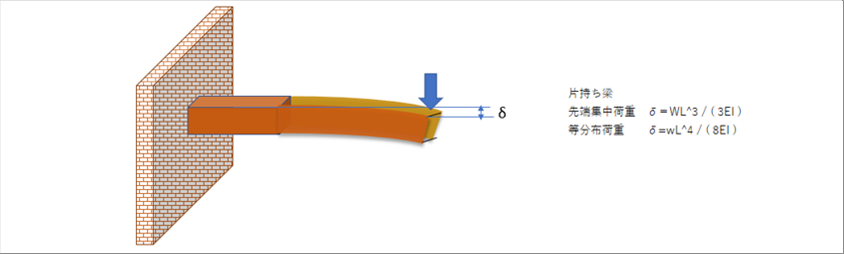単純梁　中央集中荷重　δ＝　WL^3 / ( 48EI )
単純梁　等分布荷重　　δ＝　wL^4 / ( 384EI )
●
応力集中は常時発生しています。
部材には、目的に応じてコーナー部や、ボルト穴等があります。また、何らかの原因で、使用中に傷ついたり、腐食したりして切り欠きができます。さらに、何度も使うと疲労亀裂が発生したりします。液体中では、気泡がつぶれるときに発生するキャビテーションによる損傷もあります。これらはすべて物体の形状を変化させます。
このように、大きなものや、初めはミクロンオーダーの小さなものがありますが、形状が一様でない部分に応力が集中します。
●　応力集中係数α＝最大応力σmax/平均応力σ
一般的に、αは２から５程度の場合が多い。
クリープは、高温下で、一定の荷重を加えると、時間とともに物体が変形する現象です。
疲労は、弾性限度内でも、繰り返し荷重を加えると変形が元に戻らず、最終的には破壊に至る場合もあります。
物体は、熱により膨張、収縮をするが、何らかの形で拘束されると、その時の熱ひずみに応じた応力が発生します。
計算方法は、まず膨張、収縮による変位量を計算する。実際の変位量は、拘束条件によるので、計算変位量と拘束条件の差が、それぞれ圧縮応力、引張応力を発生させます。
延びλ=lαΔt
熱応力σ=Eε=EαΔt
l?: 棒の長さ、α: 線膨張係数、Δt: 温度変化
線膨張係数 α(x 10-6/K)　→　１ｍあたり1℃(K)でαμm伸縮する。 炭素鋼 α=12.5
完全に均一な材質で、完全に均一な形状で、完全に物体の軸と圧縮荷重の軸が一致していれば発生しないが、現実にはこのような条件はありえない。
細長い物体に圧縮荷重をかけた場合、ある時点で、荷重の方向とは直角の方向に曲がってしまうこと。曲がった結果、弾性変形に収まらず、塑性変形をする場合もある。
座屈荷重はヤング率と断面二次モーメントに比例し、長さの二乗に反比例する。普通の日本語で言えば、「硬くて太いと座屈しにくく、長いと急に座屈しやすくなる。」となります。
Author: T. Oda
このページは、excel2webで自動作成しました。