| |
 |
| |
 |
| |
| ● 曲げ強さ 断面二次モーメント |
| (1) 断面二次モーメントって何? |
| |
| ● 曲げ強さ 断面二次モーメント I の定義式 |
| (1) 図芯周りの断面二次モーメントの定義式(オフセットなし) |
| (2) 長方形断面の断面二次モーメントの計算 |
| (3) 円形断面の断面二次モーメント |
| (4) 一般的な状態の断面二次モーメント |
| (5) オフセットした部材の断面二次モーメントの例 H鋼、I鋼 |
| |
| ● たわみ量δ の計算 |
| |
| |
| |
 |
| ● 曲げ強さ 断面二次モーメントと断面係数 |
| |
 |
| (1) 断面二次モーメントって何? |
| |
| 断面二次モーメントは、部材がどこで使われているかも加味した、曲げにくさを表し、数値が大きいほど曲げにくいとこを示しています。 |
| |
| 英語の直訳は、断面慣性モーメントで、慣性のイニシャルをとって I で表されます。 |
| |
| 断面二次モーメントは、断面の形状に、どこで使われているかの位置情報でできています。したがって、断面二次モーメントは、断面形状が変わるか、同じ断面形状で使用場所が変わると変わります。 |
| |
| 見栄えや設置可能位置の制約の範囲で、力がかかるところから離して使うほうが断面二次モーメントを大きくできるので、曲がりにくくなります。部材を使う場所での断面二次モーメントは、部材の図心を原点にした数値に、使用位置と断面積の積を加算した数値で定義されます。 |
| |
| 断面二次モーメントを使えば、具体的にどれだけ曲がるか(たわみ量)も計算可能です。 |
| |
| |
 |
| ● 曲げ強さ 断面二次モーメント I の定義式 |
| |
 |
| (1) 図芯周りの断面二次モーメントの定義式(オフセットなし) |
| |
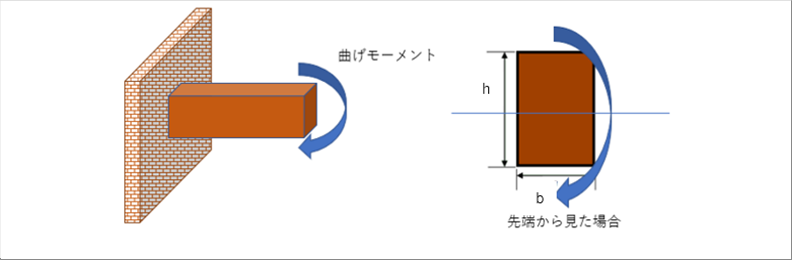
| 下図は、四角断面の部材に、上から曲げモーメントがかかっている様子を示しています。 |
| |
| 部材の使用場所は、モーメントがかかる位置ど同じ(オフセット=0)なので、図芯の周りの断面二次モーメントを計算します。 |
| |
 |
| |
| 断面二次モーメントの定義式は、曲げモーメントがかかっている位置の2乗を、断面全部で積分したものです。 |
| |
| x軸周りの断面二次モーメント Ix は、yの2乗の積分、y軸まわりの断面二次モーメント Iy は、xの2乗の積分になります。 |
| |
| モーメントがかかる方向の寸法をh、他方をbと書くことがおおいので、それに従うと、四角形、円形、円筒形の断面係数は簡単に計算できます。 |
| |
 |
| |
| 四角形 Ix = bh^3/12 |
| |
| 円形 Ix = πd^4 / 64 |
| |
| 円筒形 Ix = π(do^4 - di^4) / 64 |
| |
 |
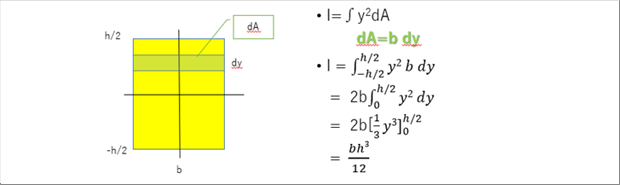
| (2) 長方形断面の断面二次モーメントの計算 |
| |
| 公式を忘れてしまった場合は、簡単に計算できます。 |
| |
| 長方形断面は、幅bが一定なので、定義式の dA は下の緑の部分になります。あとは積分するだけです。 |
| |
 |
| |
 |
| (3) 円形断面の断面二次モーメントの計算 |
| |
| 公式を忘れてしまった場合、こちらも定義式から計算できます。円形断面の式は、サイン、コサインの積分になります。 |
| |
| 三角関係の公式でよく使うもの。 |
| |
| ● サインとコサインの二乗の和は1。 |
| |
| ● 倍角の式を使った、三角関数の2乗の1乗への変換。 |
| |
 |
| |
 |
| (4) 一般的な状態の断面二次モーメント |
| |
| 実際の部材にかかるモーメントは、図芯からオフセットしている場合が多いです。 |
| |
| 簡単に計算するには、実際のx-y軸と、図芯を原点にしたu-v軸を考えて、軸の変換式を定義式に代入します。 |
| |
| uv軸は図芯にします。このため、uv軸の断面2次モーメントはゼロになります。 |
| |
 |
| |
 |
| (5) オフセットした部材の断面二次モーメントの例 H鋼、I鋼 |
| |
| 部材としてよく使用するH鋼、I鋼は、形状が決まっていて、カタログには公称断面二次モーメントが記載されているので、オフセットした一般式の例として計算した数値と比較するのにちょうどいいので、計算してみる。 |
| |
| 下のH鋼の公称断面二次モーメントは1810cm4で、計算値は1761cm4になった。計算値では、部材の断面形状だけを使ったが、部材の隅が絵のように直角になっていることはなく、実際は若干テーパー状、円弧状に部材が存在する。これらは計算では無視したので、公称値より小さくなったと思われる。 |
| |
 |
| |
| |
 |
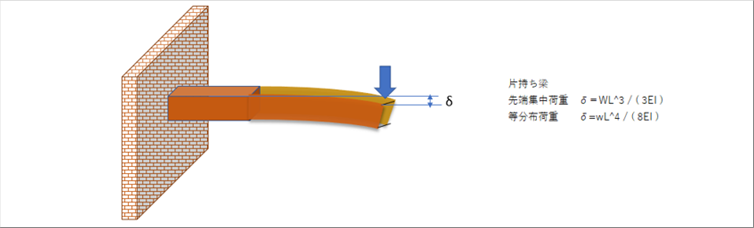
| ● たわみ量δ の計算 |
| |
| 曲げモーメントがかかっている部材のたわみ角とたわみ量は、モーメントを積分して求める。 |
| |
| 〇 たわみ角Θ = 曲げモーメントを1回積分 |
| |
| 〇 たわみ量δ = 曲げモーメントを2回積分 |
| |
| 加速度を1回積分すると速度が求められ、2回積分すると位置が計算できるが、モーメントとたわみも、これと似ている。 |
| |
 |
| |
| 単純梁 中央集中荷重 δ= WL^3 / ( 48EI ) |
| |
| 単純梁 等分布荷重 δ= wL^4 / ( 384EI ) |
| |
| |
| Author: T. Oda |
| このページは、excel2webで自動作成しました。 |