| |
 |
| |
 |
| ● 応力集中とは何でしょうか。 |
| (1) 応力集中 板に円形の穴がある場合 |
| (2) 応力集中 板にだ円形の穴がある場合 |
| (3) 応力集中 段付き板 |
| (4) 応力集中の低減 |
| |
| |
 |
| ● 応力集中とは何でしょうか。 |
| |
| 応力集中は常時発生しているといっていいと思います。 |
| |
| 部材には、目的に応じてコーナー部や、ボルト穴等があります。また、何らかの原因で、使用中に傷ついたり、腐食したりします。さらに、何度も使うと疲労亀裂が発生したり、液体中では、気泡がつぶれるときに発生するキャビテーションによる損傷もあります。これらはすべて物体の形状を変化させます。もとの形状から変化した部分に応力が集中します。 |
| |
| 変化には、はじめはミクロンオーダーの小さなものや、時間経過後に大きくなったものがあります。このように、形状が一様でない部分に応力が集中します。 |
| |
| 作った直後であっても、切削バイトの刃先の形状や、研磨砥石の小さな凸凹が表面に残るので、最初から一様な形状なものはないといっていいと思います。 |
| |
 |
| (1) 応力集中係数 |
| |
| 応力集中係数は、最大応力を平均応力で除算します。 |
| |
| 応力集中係数α=最大応力σmax/平均応力σ |
| |
| 一般的に、αは2から5程度の場合が多い。 |
| |
 |
| (2) 応力集中 板に円形の穴がある場合 |
| |
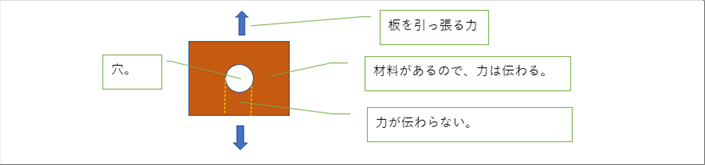
| 横幅が相当広い板の中央に丸い穴があいていて、上下から均等に引っ張っていると仮定します。 |
| |
| 穴から遠いところでは引張は上から下に伝わっていきますが、穴の位置では、上から引っ張った力は下に伝わりません。その力はどこかにかかっているはずです。一番考えやすいのは、穴のヘリに集中してかかり、穴から遠ざかるとぐっと小さくなるというイメージです。 |
| |
| 一番考えやすいのは、穴の部分のかかるはずだった力が、穴のヘリに集中してかかり、穴から遠ざかると小さくなるというイメージです。 |
| |
 |
| |
| 平均応力 σ0 = F / Bt |
| |
| 応力分布 σy = 0.5 σ0 ( 2 + a^3/x^2 + 3 a^4/x^4 ) |
| |
| 原点:円孔の中心、x>=a |
| B: 板の幅 t: 板の厚み a: 円孔の半径 b = (B-2a) |
| |
| σyは、x=a で最大値 3 σ0 となる。応力集中係数 α=3 |
| |
 |
| (3) 応力集中 板にだ円形の穴がある場合 |
| |
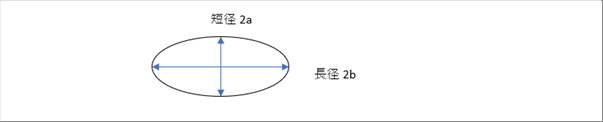
| 下図のような楕円系の穴があいているとします。 |
| |
 |
| |
| 各部の応力 σy = σ0 ( 1 + 2 SQRT ( a/ρ ) ) |
| ρ = b^2 / a 先端の曲率半径 |
| |
| 応力集中係数 α = 1 + 2 SQRT ( a/ρ ) = 1 + 2a/b |
| |
| この式では、先端の曲率半径ρが分母にあるので、曲率半径ρが小さくなると応力集中係数αは急激に大きくなることがわかります。 |
| |
| 現場的に言えば、力のかかる方向と垂直に小さなクラックがあると、クラックの先端に大きな応力集中が発生することがわかります。その結果、小さなクラックは急激に大きくなりることが予想されます。 |
| |
 |
| |
| 小さなクラックを細長い楕円と仮定して、力がかかる方向に長軸がある場合と、短軸がある場合で応力集中係数を計算してみます。 短軸2a=0.1, 長軸2b=1 |
| |
| 左図の場合は、α=1.2 ですが、右図の場合は21になります。 |
| |
| 部材に発生する平均応力が、降伏応力の10%の場合、左図では最大応力が降伏応力の12%、右図では210%になります。右図では、クラックの先端が降伏応力の2.1倍になるので、塑性変形を起こし、場合によっては破壊に至りクラックが進展すると思われます。 |
| |
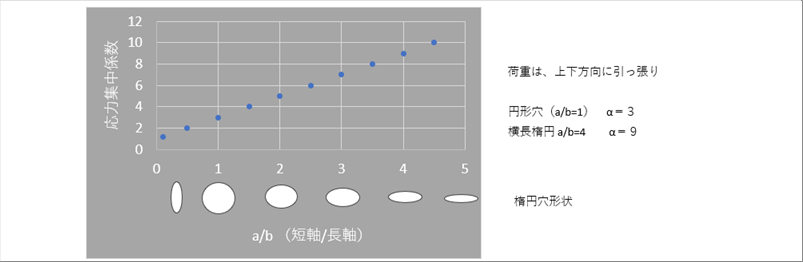
| 長径と短径の比と応力集中係数のグラフは下記になります。 |
| |
 |
| |
 |
| (4) 応力集中 段付き板 |
| |
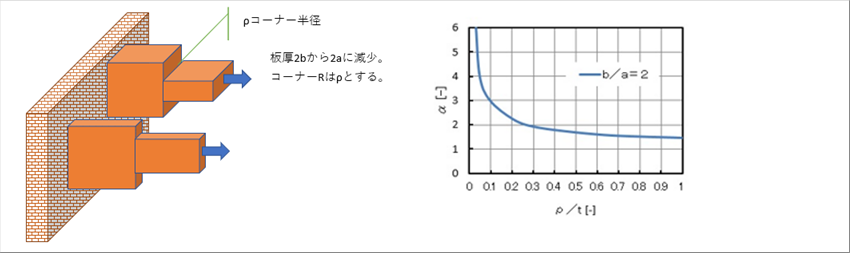
| 段付き板の応力集中係数の無次元グラフは下のようになります。 |
| |
 |
| |
| コーナー半径が小さいと大きな応力集中が発生することがわかります。 |
| |
 |
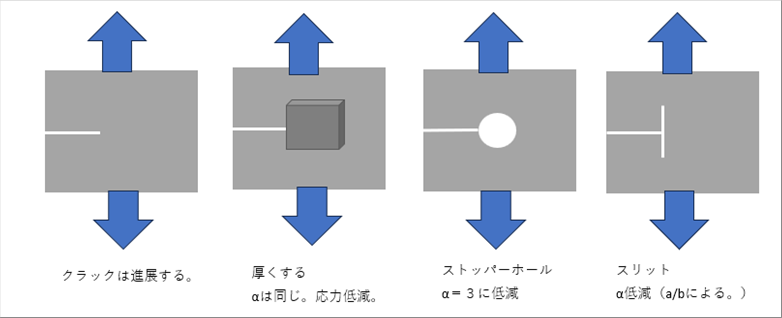
| (5) 応力集中の低減 |
| |
| 形状変更ができない場合は、応力集中係数は変わりませんが、厚みを厚くして、応力の絶対値を小さくできます。 |
| |
| 形状が変更できる場合は、コーナー半径を大きくする、荷重に垂直方向に切り欠きを追加して緩衝効果で低減するなどがあります。半径を大きくする例としては、クラックの先端にドリル穴を開ける(ストッパーホール)などがあります。 |
| |
 |
| |
| |
| Author: T. Oda |
| このページは、excel2webで自動作成しました。 |



























