| |
 |
| |
 |
| ● 数値解析が必要な理由 |
| ● 差分法と有限要素法 |
| ● 有限要素法を使う際に重要なこと |
| ー 要素分割と条件 |
| ー 要素内方程式 |
| ● 有限要素法で得られた結果の是非の判断 |
| |
| |
 |
| ● 数値解析が必要な理由 |
| |
| 熱伝導方程式などの微分方程式は、ある現象を方程式で表現しています。したがって、微分方程式が積分できれば、その現象が方程式で表現できます。 |
| |
| 微分方程式を解いたものを解析解といいます。解析解には誤差がないので大変有益です。ただし、残念なことに、熱伝導方程式のような微分方程式の解析解は、例外的に特別な場合を除き、得られません。 |
| |
| 解析解と違って、数値解析は誤差はありますが、近似解を得ることができます。有名な数値解析法は、有限要素法と差分法だと思いますが、どちらも微分方程式の近似解を数値的に得る方法です。 |
| |
| 数値解析が必要な理由は、解析解が得られない微分方程式を解くためです。 |
| |
 |
| ● 差分法と有限要素法 |
| |
| 数値解析方法は複数ありますが、差分法と有限要素法が有名です。間違っているかもしれませんが、それぞれを簡単にまとめると次のようになります。 |
| |
| 差分法は、微分の式を差分の式に直接的に置き換える方法です。 |
| |
| 具体的には、無限級数に置き換えた微分方程式の、有限個を使います。したがって、使われなかった無限級数の残分が誤差になります。 |
| |
| 誤差は差分の大きさに比例するので、差分を十分小さくすれば、誤差を無視できる程度に小さくすることができます。 |
| |
| 差分法の詳細は、シミュレーション「差分法」を参照してください。 |
| |
| 有限要素法は、物体を有限個の要素に分割し、要素内に間接的な連立方程式をたてて解く方法です。 |
| |
| したがって、どのような要素に分割したか、要素内の連立方程式は妥当か、の2点で結果が左右されます。誤差がどこにどのくらいあるかは、要素分割と連立方程式をたてた解析者が吟味する必要があります。 |
| |
| TSコンサルティングのサイトでは、有限要素法は扱っていませんので、ここで重要と思われることをまとめておきたいと思います。 |
| |
 |
| ● 有限要素法を使う際に重要なこと |
| |
| 有限要素法は、要素の分割方法と、要素内の連立方程式に使う、単純な関数の選定が大変重要なので、ベストな結果を得るためには、知識が重要になります。 |
| |
| 利用できるプログラムが市販、提供されているので、自分でプログラムを作ることはあまりないと思いますが、知っていて損はないのでまとめてみたいと思います。 |
| |
 |
| 〇 要素分割と条件 |
| |
| 例えば、構造解析に使う場合は、構造物のどこをどのくらいの大きさ、形状、個数の要素に分割するのが最適かが重要です。物体に外から作用している力があれば、どの要素にどれくらいで割り振るかなどが結果を左右します。 |
| |
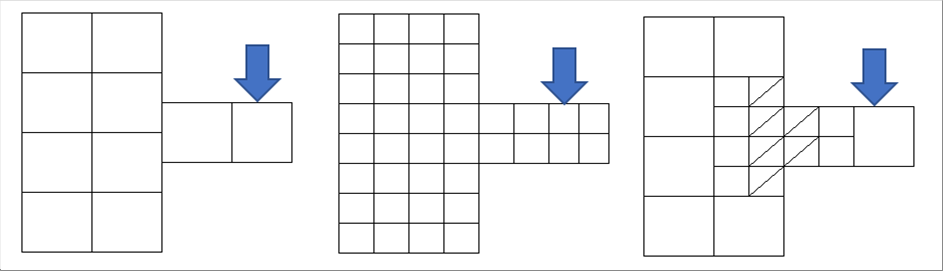 |
| |
| 上の3個は、形状は同じですが、粗く分割した場合、細かく分割した場合、変形が集中すると思われる部分を細かく、かつ3角形の要素にした場合を示しています。 |
| |
| 突出し部分にかかる荷重は、「集中荷重」で、1点でかかっています。荷重点近傍の突出し部の変形を知りたい場合は、細かくする部分を変えるほうがいいと思います。 |
| |
| また、「集中荷重」であっても、実際はある大きさをもったものでその物体に伝えられます。したがって、1点にかけるのが正しいかどうかの判断も必要です。実際の大きさを反映したほうが良い結果が得られると推測されます。 |
| |
| 塑性加工解析に使う場合は、塑性加工の知識をもとに、変形が大きいと推測される部分を適切に分割することも重要です。 |
| |
| 構造解析と違って、塑性加工の解析では、外力をかけるのではなく、その加工をしたらどのくらいの反力になるのかを計算したい場合があります。この場合は、外力は条件ではなく、解析結果になります。 |
| |
| ロールでプレートを圧延する場合の要素の分割は、下記のようにいくつか考えられるので、解析目的に合ったものを使う必要があります。 |
| |
 |
| |
 |
| 〇 要素内方程式 |
| |
| 要素内方程式に使う式は、決まりはないので、応用範囲は広いですが、専門知識が必要になります。 |
| |
| 計算がしやすいように1次(線形)にしてもいいですが、材料力学、熱力学、流体力学、塑性加工学など、解析内容に最適な知見をもとに決めることも重要になります。 |
| |
| 例えば弾性変形は線形ですが、弾性限度を超えた塑性加工の領域では非線形になります。熱伝導方程式も非線形です。流体力学の運動方程式であるナビエストークスの方程式も非線形です。 |
| |
| 非線形な要素内方程式を間接的に表す例として、エネルギーを考える場合があります。物体はエネルギーが最小になるように変形するので、変形の計算の代わりに、エネルギー最小化の計算をする選択をすることもできます。 |
| |
| 塑性変形を知るために、塑性エネルギーを変位か速度であらわし、加工エネルギー、摩擦損失エネルギーなどの全エネルギーを最小化する方法があります。複数の変数の最小化には、偏微分方程式を解くことになるので、偏微分方程式が1次式(線形)だとそのあとの計算が便利になります。 |
| |
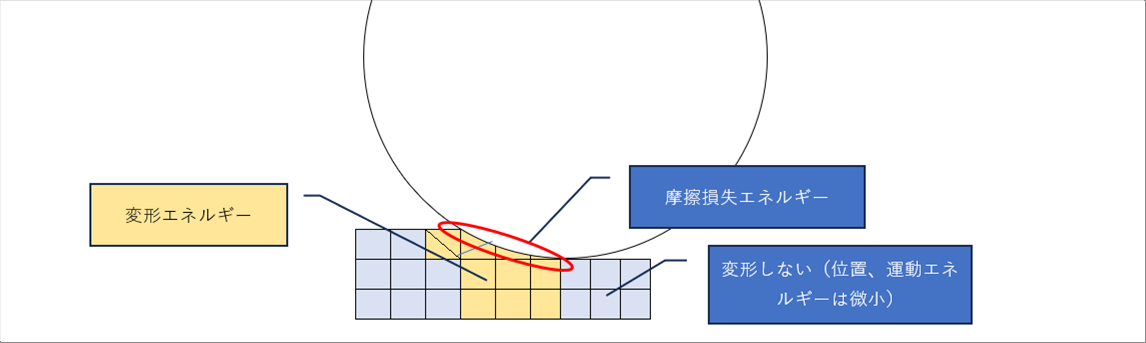 |
| |
| 温度解析に使う場合は、熱伝導方程式を適用する際に、解析する対象内部の温度推定式があれば便利です。温度推定式は、実験式などが使われると思いますが、温度推定式の精度などが、結果を左右します。 |
| |
| 温度解析の場合も、計算方法として、これらの要素内方程式が連立1次方程式にできると、線形代数の解の公式が使えるので便利です。 |
| |
 |
| ● 有限要素法で得られた結果の是非の判断 |
| |
| このように、有限要素法を使ってえられた数値解は、使う人の知識と使用した要素分割、簡単な連立方程式、外部からかかる力、熱などの境界条件の与え方で変わって来ます。 |
| |
| したがって、結果の是非、妥当性の判断が重要になります。 |
| |
| 実験や、実勢の設備で計測して得られた結果と比較して判断するのがいいと思いますが、このためには、数値解をグラフ化、3D化などで可視化すると、妥当性を迅速に判断するのに役に立つと思います。 |
| |
| Author: T. Oda |
| このページはエクセルで作り、excel2webでhtmlとcssを自動作成しました。 |
| |





















