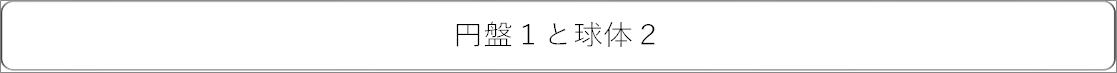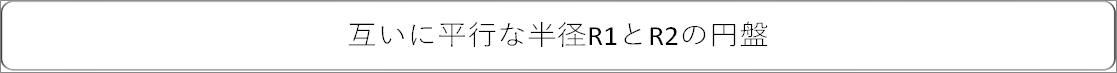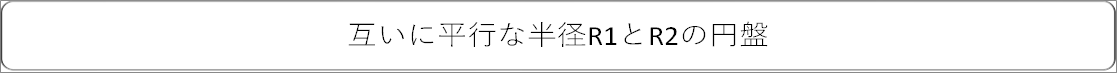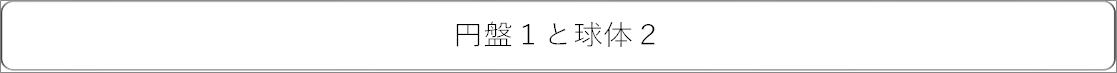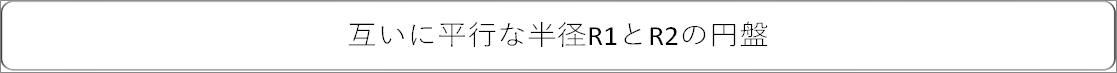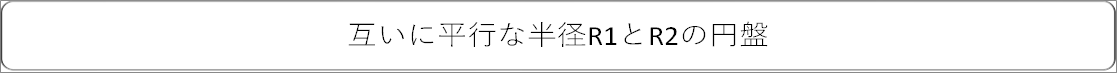| |
 |
| |
 |
| ● 形態係数って何 |
| ● 定義式 |
| 形態係数=ターゲットの入力エネルギー / ソースの全エネルギー |
| ● 代表的な形状の形態係数の計算結果 |
| 円盤から球(球から円盤) |
| 同形状長方形 |
| 異径円盤 |
| 垂直な長方形 |
| ● 形態係数の実炉への適用 |
| 回転炉床式加熱炉、熱処理炉の形態係数計算例 |
| |
 |
| ● 形態係数って何 |
| |
| 形態係数は、熱輻射の計算に大変重要な係数です。 |
| |
| 熱輻射は、すべての物体が絶対温度の4乗に比例した電磁波を放出することで発生します。(詳細は「基礎」と「熱輻射」参照願います。) 黒体の場合は比例定数はボルツマン係数ですが、実際の物体では、さらに物体の表面積、輻射率、熱源と物体との位置関係を考慮して乗算する必要があります。 |
| |
| 熱源と物体との位置関係を、形態係数という数値で表します。形態係数は、熱源・物体の形状と配置によって計算するので、必要に応じた図面が必要になります。例えば、これから解析する加熱炉、熱処理炉の構造図と被加熱材の形状と置く場所などです。 |
| |
| 熱輻射が炉内でどのように働いているかですが、まず、熱輻射の実態は電磁波です。電磁波は、熱源から直進し、炉内の吊りもの、でっぱり、凹凸などの障害物に当たると反射します。したがって、被加熱材から見れば、「影」になる部分が発生し、熱源からの電磁波が届かないか減衰して届くことになります。 |
| |
| 下の絵は、赤が熱源で、黒が物体をあらわしています。左の絵では、物体表面のある点は、遮蔽物が無いので熱源全体から熱輻射を受けています。右の絵では、熱源t物体の間に遮蔽物があるので、熱源の一部から熱輻射が届きません。 |
| |
 |
| |
| 大型の加熱炉、熱処理炉では、複数の物体を同タイミングで加熱する場合がありますが、その場合、物体が炉内で移動して連続処理をしている場合は、物質と炉内構造物の相対的な配置が時々刻々変化します。すなわち、輻射熱を受ける物体から見れば、炉内の位置が変わるので、形態係数も時々刻々変化することになります。 |
| |
| 電磁波の進行をレイトレーシングのようにあつかうのか、炉内の場所ごとの形態係数をあらかじめ計算しておくのか、ある範囲の中間地点などを代表点にして、その範囲にいるときは同じ形態係数をつかうのか、など、熱輻射の扱い方はいろいろ考えられますので、どのような方法にするのかは、関係者で合意しておいたほうがいいと思います。 |
| |
| 例えば、数値計算の陽解法は、時間変化を順に追っていく方法なので、形態係数をその都度計算できますが、計算の目的によっては、計算方法を簡略化することも可能だと思われます。 |
| |
 |
| ● 形態係数の定義式 |
| |
| 形態係数は、立体角を用いて、視野の範囲を計算します。詳細は省略しますが、重要なので、概要を順に説明します。 |
| |
| 形態係数は、熱源(ソース)から出て、ターゲット(被加熱材)に入るエネルギーと、ソースの全放射エネルギーの比率で定義されます。 |
| |
 |
| |
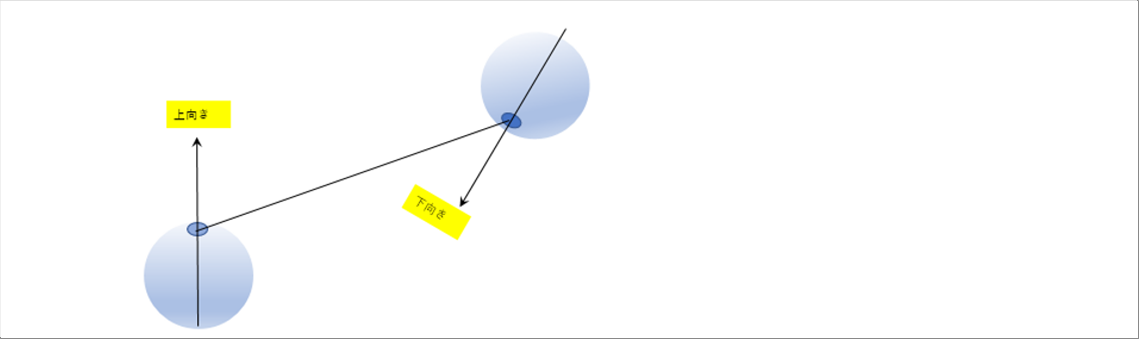
| 熱源(ソース)と物体(ターゲット)の一般的な位置関係は次のようになります。最低限、お互いが向き合っている必要があります。 |
| |
 |
| |
| 下の目玉を1,右上の目玉を2とします。黒目部分が微小面積dAとします。この時放射強度Eと放射エネルギーQは、次のようになります。 |
| |
| E = σT^4 |
| dQ = πEdA |
| Q = πEA |
 |
| |
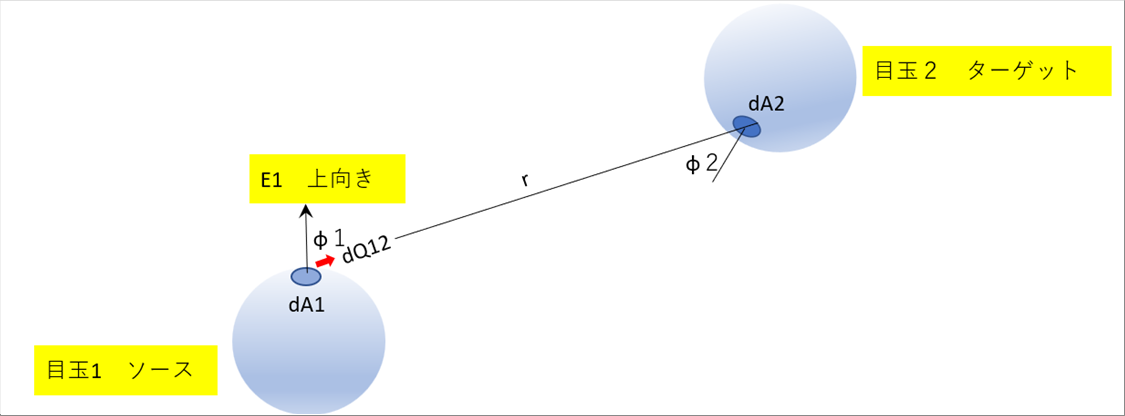
| ソースの鉛直線からターゲットの角度がφ1、ターゲットの鉛直線からソースの角度がφ2とします。ソースからターゲットの微小面積に入る熱量はdQ12で表します。 |
| |
 |
| |
| 放射エネルギdQ1、右上の目玉2の微小面積dA2 に入る熱量dQ12は立体角Ω(オメガ)を使って次のように定義されます。 |
| |
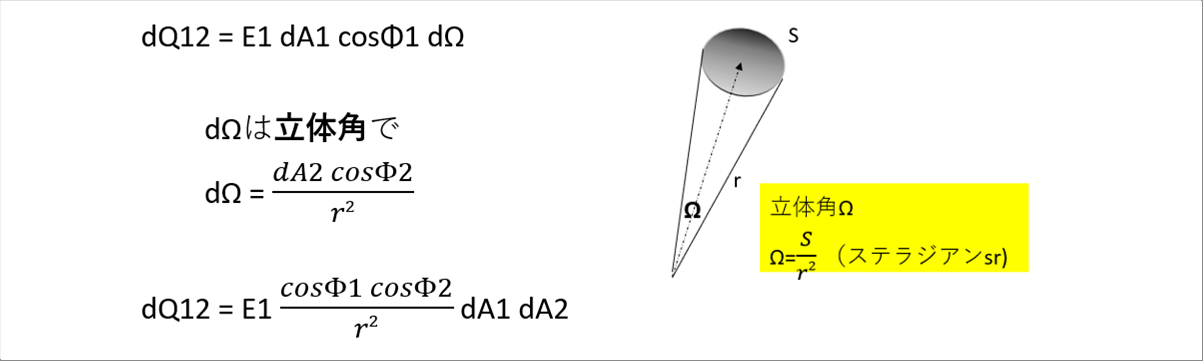 |
| |
| 目玉2がソース、目玉1がターゲットの熱輻射も同時に発生しています。 |
| |
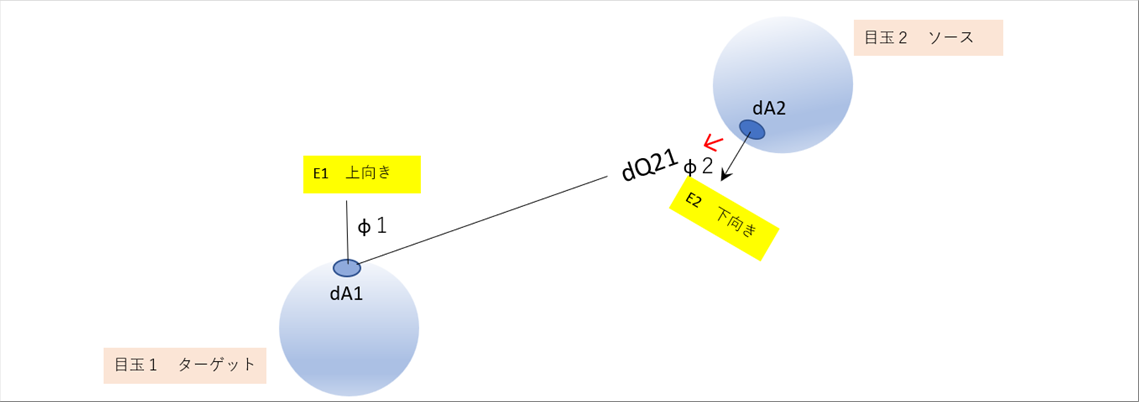 |
| |
| dQ21は、次式で与えられます。 |
| |
 |
| |
| 形態係数の定義式 F12 = Q12 / Q1 、F21 = Q21 / Q1 に上の式をあてはめます。 |
| |
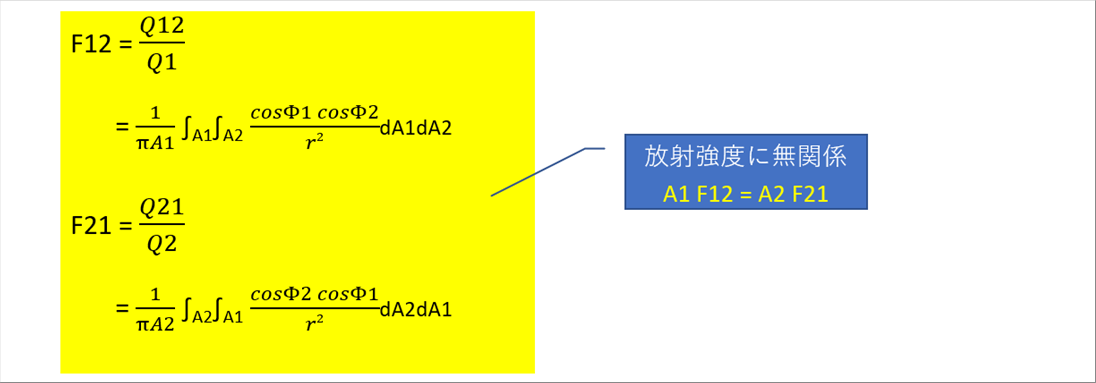 |
| |
| 形態係数は、放射強度に無関係で、ソースとターゲットの面積と、相対的な角度のみに依存します。また、ソースとターゲットの形態係数は、どちらかがわかれば、もう一方は面積比で簡単に計算できます。 |
| |
| 位置関係がわかりやすいようにアイボールを使いましたが、立方体でも同じ関係式が成り立ちます。 |
| |
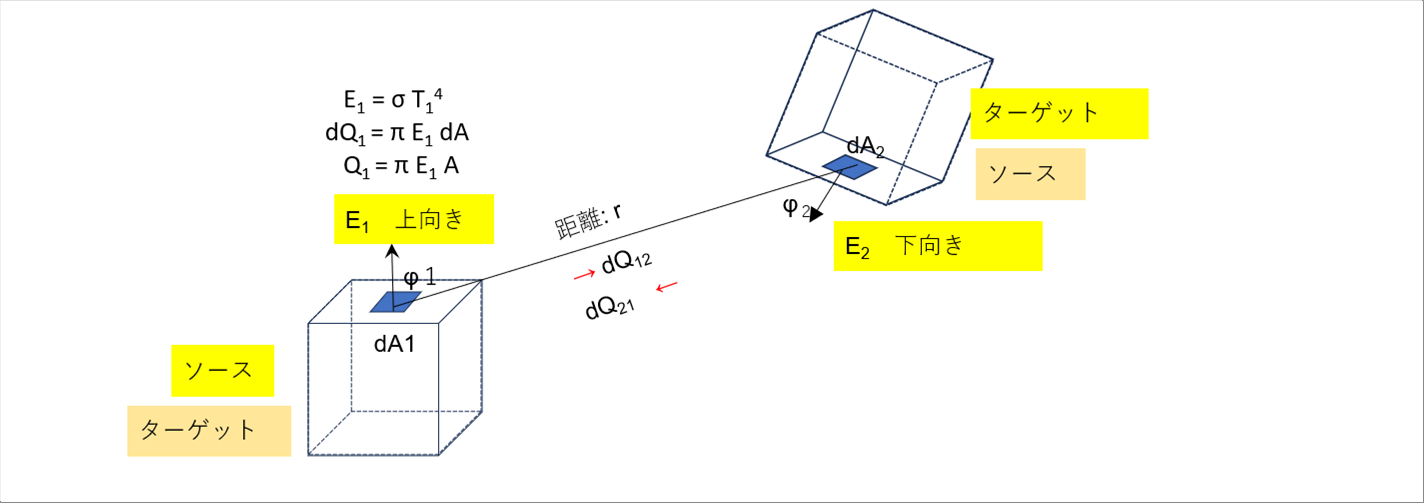 |
| |
 |
| ● 代表的な形状の形態係数の計算結果 |
| |
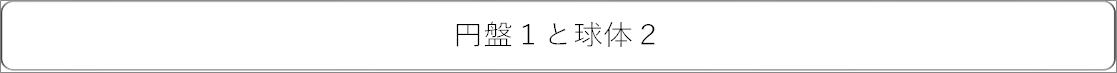 |
| 円盤1と球体2 |
| |
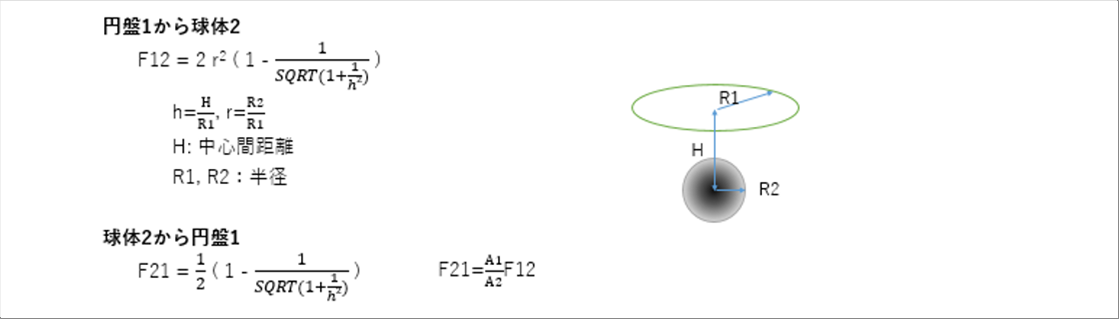 |
| |
 |
| 同形状の長方形1,2 |
| |
 |
| |
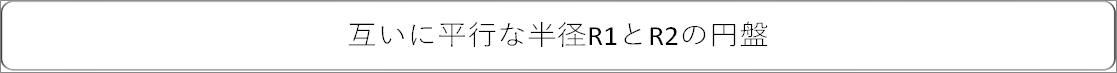 |
| 互いに平行な半径R1とR2の円盤 |
| |
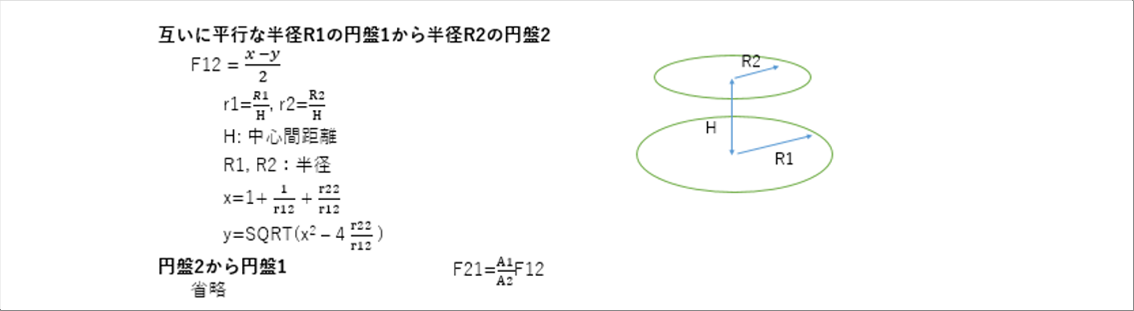 |
| |
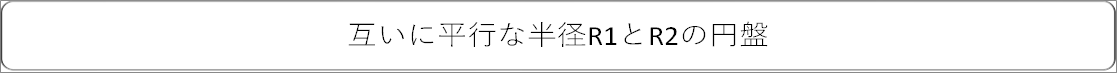 |
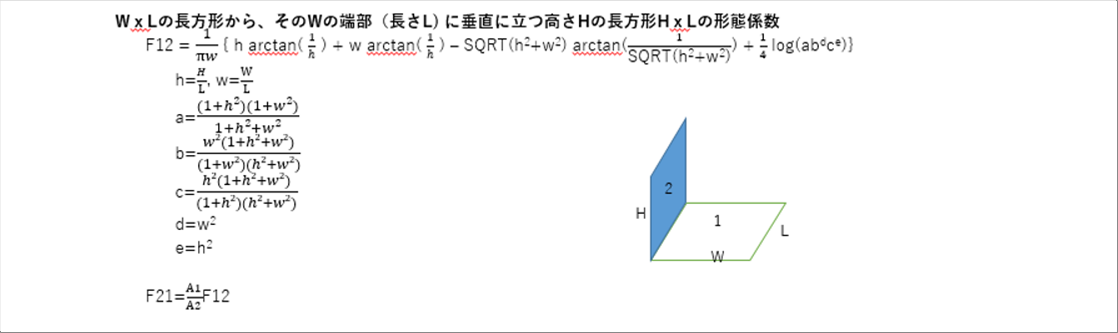
| お互いに垂直な長方形 |
| |
 |
| |
 |
| ● 形態係数の実炉への適用 |
| |
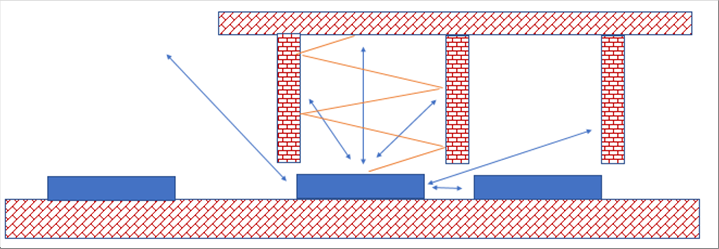
| 実際の加熱炉はウォーキングビーム方式や、回転炉床方式など、その内部は例で紹介した形状より複雑な形状をしている。炉内の形状を図面をもとに、どう取り扱うかよく検討して、形態係数を決めるのがいいと思われる。 |
| |
 |
| |
| 方法が決まれば、その都度オンラインで計算してもいいし、ポジションごとに事前にDB化しておく方法もあると思います。 |
| |
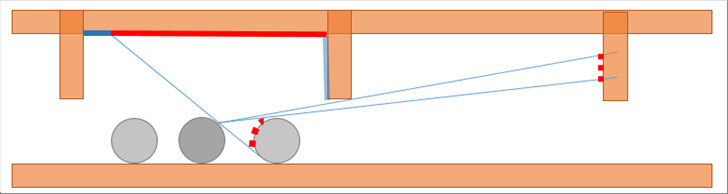
| 被加熱材が丸鋼片である場合は、同様に次のようになると思われる。 |
| |
 |
| |
| 前後のゾーンのバッフル、天井は距離が遠いか見通しがほぼできないことから無視。隣接する別の被加熱材とは温度差がほとんどないので無視。自ゾーンのバッフルは形態係数的に傾斜があるので、天井部分の死角部分と相殺していると考えるなどが考え方としてあると思う。ほかの仮定を採用しても問題ないので、解析したい場所に最適と思われる条件を検討することが重要といえる。 |
| |
 |
| ● 回転炉床式加熱炉、熱処理炉の形態係数計算例 |
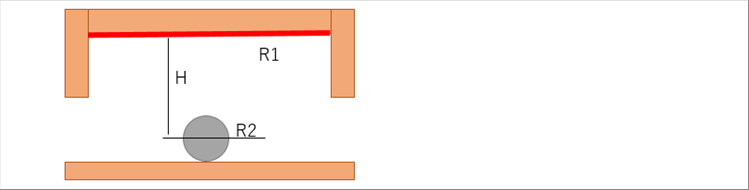 |
| 天井は円盤と仮定して積分を解くと |
| |
 |
| |
| ゾーン幅3000mm, 天井1000mm, 外径170mmのときF12=0.003078 |
| ゾーン幅3000mm, 天井1000mm, 外径170mmのときF21=0.2396 |
| |
| |
| |
| Author: T. Oda |
| このページは、excel2webで自動作成しました。 |